题目内容
观察下列等式：
，
，
，…
（1）猜想并写出第n个等式为：______；（n为正整数）
（2）证明你写出的等式的正确性；
（3）补全第2012个等式：2012-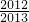
=______．
解：（1）根据上述一系列等式得到第n个等式为n-
=n•；
（2）证明：∵左边=n-=
-=
，
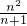右边=n•=，
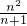∴左边=右边，即等式成立；
（3）2012-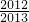=2012×．
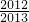故答案为：（1）n-=n•；（3）2012×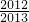
分析：（1）根据上述一系列等式得到第n个等式为n-=n•；
（2）左边两项通分并利用同分母分式的减法法则计算，右边利用乘法法则计算，得到结果相等，可得出等式成立；
（3）令n=2012代入（1）得到的规律中，即可得到所填空的结果．
点评：此题考查了分式的混合运算，属于规律型题，弄清题中的规律是解本题的关键．
=n•；（2）证明：∵左边=n-
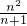=-=，右边=n•
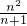=，∴左边=右边，即等式成立；
（3）2012-
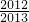=2012×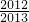．故答案为：（1）n-
=n•；（3）2012×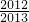分析：（1）根据上述一系列等式得到第n个等式为n-
=n•；（2）左边两项通分并利用同分母分式的减法法则计算，右边利用乘法法则计算，得到结果相等，可得出等式成立；
（3）令n=2012代入（1）得到的规律中，即可得到所填空的结果．
点评：此题考查了分式的混合运算，属于规律型题，弄清题中的规律是解本题的关键．
练习册系列答案
相关题目