题目内容

（1） $数学公式$
（2）（ $数学公式$ +2）（ $数学公式$ -2）
（3）已知 $数学公式$ x=1+2x，求x²-4x-3的值．

解：（1）原式= $\text{[math]}$ ÷（- $\text{[math]}$ ）+ $\text{[math]}$ ÷（- $\text{[math]}$ ）
=- $\text{[math]}$ - $\text{[math]}$ ；

（2）原式=（ $\text{[math]}$ ）²-2²
=a-4；

（3）∵ $\text{[math]}$ x=1+2x，
∴x= $\text{[math]}$ = $\text{[math]}$ +2，
∴x²-4x-3
=x²-4x+4-7
=（x-2）²-7
=（ $\text{[math]}$ +2-2）²-7
=5-7
=-2．
分析：（1）根据多项式除以单项式法则展开，求出即可；
（2）根据平方差公式求出即可；
（3）求出x的值，再代入求出即可．
点评：本题考查了二次根式的混合运算，平方差公式，完全平方公式的应用，主要考查学生的计算能力．

练习册系列答案

暑假衔接培优教材浙江工商大学出版社系列答案

暑假作业快乐的假日系列答案

欣语文化快乐暑假沈阳出版社系列答案

暑假作业辽海出版社系列答案

暑假作业合肥工业大学出版社系列答案

小小全能王衔接教材内蒙古大学出版社系列答案

暑假作业本大象出版社系列答案

暑假期导航学年知识大归纳系列答案

新课堂假期生活寒假用书北京教育出版社系列答案

假期伙伴暑假大连理工大学出版社系列答案

相关题目

不等式-2x+4＞0的解集是________．

根据《最新刑法修正案（八）》醉酒驾驶机动车的部分行为被纳入刑罚处罚条例，为了配合该项新规落实，某校组织了部分同学在“人文社区”开展了“你最支持哪种戒酒方式”的问卷调查，并将调查结果整理制成了如图所示的统计图：

（1）此次调查中一共调查了多少人？
（2）请把两种统计图补充完整，求出替代品戒酒的圆心角度数，并写出这五种戒酒方式的人数的中位数．
（3）若被调查的人中药物戒酒，警示戒酒，替代品戒酒，强制戒酒成功率分别为30%，20%，20%，30%，则
1200人中戒酒不成功的人数（含不愿戒酒的人）约为______人．

直角三角形两直角边长分别为2 $数学公式$ 和5 $数学公式$ ，则它的周长为

A.
4 $数学公式$ +5 $数学公式$
B.
5 $数学公式$ +2 $数学公式$ $数学公式$
C.
4 $数学公式$ +10 $数学公式$
D.
4 $数学公式$ +5 $数学公式$ 或2 $数学公式$ +11 $数学公式$

按如图所示的规律用同样规格的黑白两色正方形瓷砖铺设矩形地面，请观察下列图形，并解答下面问题：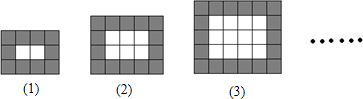

（1）将下表填写完整
图形编号（1）（2）（3）（4）   …
黑色瓷砖的块数 10 14 18   …
白色瓷砖的块数 2 6 12   …
（2）第（n）个图形中，共有黑色瓷砖块，共有白色瓷砖块；（用含n的代数式表示，答案直接写在题中横线上）；
（3）如果每块黑色瓷砖12元每块白瓷砖10元，求购买铺设第（8）个图形所需瓷砖的费用；
（4）是否存在第（n）个图形，该图形所需白、黑瓷砖的总数为18325块？若存在，求出该图形的编号n；若不存在，请说明理由．

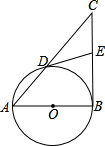如图，以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D，E为BC边的中点，连接DE．
（1）DE与⊙O什么位置关系？并说明理由．
（2）连接OE、AE，当△ABC满足什么条件时，四边形AOED是平行四边形？在此条件下，sin∠CAE的值是多少？

为从小明和小刚中选出一人去观看元旦文艺汇演，现设计了如下游戏，规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法说明这个游戏是否公平．

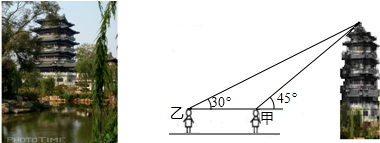如图所示，江北第一楼--超然楼，位于济南大明湖畔，始建于元代，是一座拥有近千年历史的名楼．某学校九年级数学课外活动小组的学生准备利用假期测量超然楼的高度，在大明湖边一块平地上，甲和乙两名同学利用所带工具测量了一些数据，下面是他们的一段对话：
甲：我站在此处看楼顶仰角为45°．
乙：我站在你后面37m处看楼顶仰角为30°．
甲：我的身高是1.7m．
乙：我的身高也是1.7m．
请你根据两位同学的对话，参考右面的图形计算超然楼的高度，结果精确到1米．（请根据下列数据进行计算 $数学公式$ ）

已知tan∠AOB= $数学公式$ ，P、Q分别是射线OA、OB上的两个动点（都不与O点重合），则 $数学公式$ 的最小值是________．