题目内容
如图所示，△ABC中，点P，Q，R分别在AB，BC，CA边上，且AP=
，BQ=
BC，CR=
CA，已知阴影△PQR的面积是19cm2，则△ABC的面积是（ ）
A．38
B．42.8
C．45.6
D．47.5
【答案】分析：通过求出△QPR的面积和△ABC面积的比，即可求出△ABC的面积．
解答：
解：过P作PM⊥BC于M，过A作AN⊥BC于N
∴△BMP∽△BNA
∴PM：AN=BP：BA=2：3
设△ABC的面积为S，则S△BQP=
BQ•PM=
•（
BC）•（
AN）=
BC•AN•
=
S
同理可得出：S△QRC=
S，
同理，过P作PE⊥AC于E，过B作BF⊥AC于F．
则S△APR=
S
S阴影=S-S△BQP-S△QRC-S△APR=
S=19
∴△ABC的面积S=12×19÷5=45.6．
故选C．
点评：已知部分求整体，可通过求得部分占整体的比重来求出整体的值．
解答：
解：过P作PM⊥BC于M，过A作AN⊥BC于N∴△BMP∽△BNA
∴PM：AN=BP：BA=2：3
设△ABC的面积为S，则S△BQP=
BQ•PM=•（BC）•（AN）=BC•AN•=S同理可得出：S△QRC=
S，同理，过P作PE⊥AC于E，过B作BF⊥AC于F．
则S△APR=
SS阴影=S-S△BQP-S△QRC-S△APR=
S=19∴△ABC的面积S=12×19÷5=45.6．
故选C．
点评：已知部分求整体，可通过求得部分占整体的比重来求出整体的值．
练习册系列答案
相关题目
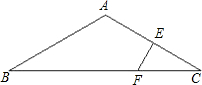如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=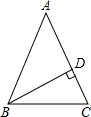
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．