题目内容

伟大的数学家欧拉发现并证明的关于一个多面体的顶点（V）、棱数（E）、面数（F）之间关系的公式为________．

V+F-E=2
分析：根据一个多面体的顶点、面数、棱数的关系：顶点+面数-棱数=2，列出公式即可．
解答：伟大的数学家欧拉发现并证明的关于一个多面体的顶点（V）、棱数（E）、面数（F）之间关系的公式为V+F-E=2．
点评：熟记一个多面体的顶点、面数、棱数的关系式：顶点+面数-棱数=2．

练习册系列答案

点对点决胜中考系列答案

新年晚会是我们最欢乐的时候，会场上，悬挂着五彩缤纷的小装饰品，其中有各种各样的立体图形．

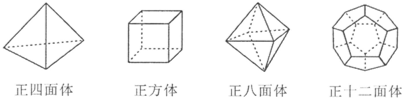
请你数一下上面图中每一个立体图形具有的顶点数（v）、棱数（e）和面数（f），并将结果记入下表中：
名称各面形状顶点数（v）棱数（e）面数（f）
正四面体正三角形
正方体正方形
正八面体正三角形
正十二面体正五边形
伟大的数学家欧拉发现了f、e、v之间存在着一个奇妙的相等关系．根据上面的表格，你能归纳出这个相等关系吗？