题目内容
8.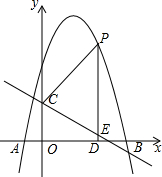 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(5,0),直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方抛物线上一个动点,过P作PE⊥x轴交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(5,0),直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方抛物线上一个动点,过P作PE⊥x轴交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;
(2)当m=$\frac{9}{2}$时,在抛物线的对称轴上找一点G,使PG+GB最小,求点G的坐标;
(3)若E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,求出点P的坐标;若不存在,说明理由.
分析 (1)利用交点式求抛物线解析式;
(2)先利用二次函数的性质求出抛物线的对称轴为直线x=2,再利用二次函数图象上点的坐标特征求出P($\frac{9}{2}$,$\frac{11}{4}$),如图1,由于点A与点B关于直线x=2对称,连结PA交直线x=2于点G,则PG+BG=GA+GP=AP,根据两点之间线段最短得到此时PG+GB最小,接着利用待定系数法求出直线PA的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,然后计算自变量为2的函数值即可得到点G的坐标;
(3)如图2,根据二次函数图象上点的坐标特征和一次函数图象上点的坐标特征,设P(x,-x2+4x+5),E(x,-$\frac{3}{4}$x+3),则可计算出PE=|-x2+$\frac{19}{4}$x+2|,接着求出C(0,3),于是可计算出CE=|$\frac{5}{4}$x|,然后利用对称的性质和平行线的性质证明PE=CE,所以|-x2+$\frac{19}{4}$x+2|=|$\frac{5}{4}$x|,即-x2+$\frac{19}{4}$x+2=±$\frac{5}{4}$x,再分别解方程求出x得到P点坐标,当点E与C重合,易得P点坐标为(0,5).
解答  解:(1)抛物线解析式为y=-(x+1)(x-5)=-x2+4x+5;
解:(1)抛物线解析式为y=-(x+1)(x-5)=-x2+4x+5;
(2)∵y=-x2+4x+5=-(x-2)2+9,
∴抛物线的对称轴为直线x=2,
∵x=$\frac{9}{2}$时,y=-x2+4x+5=$\frac{11}{4}$,
∴P($\frac{9}{2}$,$\frac{11}{4}$),
如图1,点A与点B关于直线x=2对称,连结PA交直线x=2于点G,此时PG+GB最小,
设直线PA的解析式为y=kx+n,
把P($\frac{9}{2}$,$\frac{11}{4}$),A(-1,0)分别代入得$\left\{\begin{array}{l}{\frac{9}{2}k+n=\frac{11}{4}}\\{-k+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴直线PA的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,
∵当x=2时,y=$\frac{1}{2}$x+$\frac{1}{2}$=$\frac{3}{2}$,
∴点G的坐标为(2,$\frac{3}{2}$);
(3)如图2,设P(x,-x2+4x+5),则E(x,-$\frac{3}{4}$x+3),
∴PE=|-x2+4x+5-(-$\frac{3}{4}$x+3)|=|-x2+$\frac{19}{4}$x+2|,
当x=0时,y=-$\frac{3}{4}$x+3=3,则C(0,3),
∴CE=$\sqrt{{x}^{2}+(-\frac{3}{4}x+3-3)^{2}}$=|$\frac{5}{4}$x|,
∵E′是点E关于直线PC的对称点,
∴PE=PE′,∠EPC=∠E′PC,CE′=CE,
∵PE∥CE′,
∴∠E′CP=∠EPC,
∴∠E′CP=∠E′PC,
∴E′C=E′P,
∴PE=CE,
∴|-x2+$\frac{19}{4}$x+2|=|$\frac{5}{4}$x|,即-x2+$\frac{19}{4}$x+2=±$\frac{5}{4}$x,
当-x2+$\frac{19}{4}$x+2=$\frac{5}{4}$x,解得x1=-$\frac{1}{2}$,x2=4,此时P点坐标为($\frac{1}{2}$,$\frac{11}{4}$),(4,5);
当-x2+$\frac{19}{4}$x+2=-$\frac{5}{4}$x,解得x1=3-$\sqrt{11}$,x2=3+$\sqrt{11}$(舍去),此时P点坐标为(3-$\sqrt{11}$,2$\sqrt{11}$-3),
当点E与C重合,E关于PC的对称点E'与E重合,此时点P在y轴上,其坐标为(0,5),
综上所述,符合条件的点P为($\frac{1}{2}$,$\frac{11}{4}$),(4,5),(3-$\sqrt{11}$,2$\sqrt{11}$-3),(0,5).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和对称的性质;理解坐标与图形性质,会利用两点间的距离公式计算线段的长;会解决最短路径问题;熟练一元二次方程的解法.

| A. | (a3)2=a5 | B. | ($\frac{1}{2}$a3b)2=$\frac{1}{4}$a6b2 | C. | (-x-y)2=x2-2xy+y2 | D. | (-a-b)(a+b)=a2-b2 |
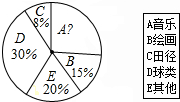 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):“最喜欢的文体活动”调查统计表
| 项目 | A音乐 | B绘画 | C田径 | D球类 | E其他 |
| 频数 | 正正正正正正 | ||||
| 人数(人) | 20 |
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
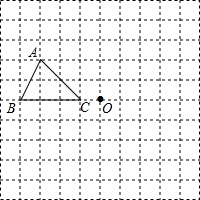 在如图的方格中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点)
在如图的方格中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点)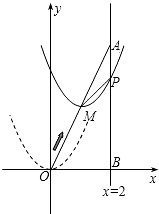 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.



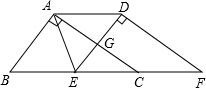 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:
如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论: