��Ŀ����
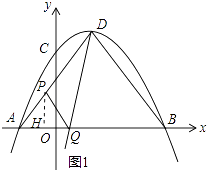
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=�� ![]() x2+bx+c��x�ύ���A����3��0������B��9��0������y�ύ���C������ΪD������AD��DB����PΪ�߶�AD��һ���㣮
x2+bx+c��x�ύ���A����3��0������B��9��0������y�ύ���C������ΪD������AD��DB����PΪ�߶�AD��һ���㣮
��1���������ߵĽ���ʽ��
��2������P��BD��ƽ���ߣ���AB�ڵ�Q������DQ����AQ=m����PDQ�����ΪS����S����m�ĺ�������ʽ���Լ�S�����ֵ��
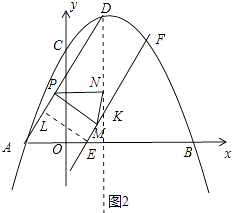
��3����ͼ2�������߶Գ�����x�ύ���G��EΪOG���е㣬FΪ��C����DG�ԳƵĶԳƵ㣬����P�ֱ���ֱ��EF��DG�Ĵ��ߣ�����ΪM��N������MN������PMNΪ����������ʱ�����ʱEM�ij���
���𰸡�
��1��
�⣺��a=�� ![]() ����������x�ύ���A����3��0������B��9��0����
����������x�ύ���A����3��0������B��9��0����
����Լ��������߽���ʽΪy=�� ![]() ��x+3����x��9��=��
��x+3����x��9��=�� ![]() x2+
x2+ ![]() x+6��
x+6��
�������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+6
x+6
��2��
�⣺��y=�� ![]() x2+
x2+ ![]() x+6=��
x+6=�� ![]() ��x��3��2+8��
��x��3��2+8��
�ඥ��D���꣨3��8����
��AD=DB=10��
���DAB=��DBA��
��PQ��BD��
���PQA=��DBA��
���PAQ=��PQA��
��PA=PQ��
���PAQ����������
��PH��AQ��H����AH=HQ= ![]() ����ͼ1�У���
����ͼ1�У���
��tan��DAB= ![]() =
= ![]() ��
��
��PH= ![]() m��
m��
��S=S��ADQ��S��APQ= ![]() m8��
m8�� ![]() m
m ![]() m=��
m=�� ![]() m2+4m=��
m2+4m=�� ![]() ��m��6��2+12��
��m��6��2+12��
�൱m=6ʱ��S���ֵ=12
��3��
�⣺��E�� ![]() ��0����F��6��6����
��0����F��6��6����
��ֱ��EF����ʽΪy= ![]() x��2��ֱ��AD����ʽΪy=
x��2��ֱ��AD����ʽΪy= ![]() x+4��
x+4��
��EF��AD����EL��AD��L������ͼ2�У�
��AE= ![]() ��sin��DAB=
��sin��DAB= ![]() ��
��
��LE= ![]() ��
�� ![]() =
= ![]() =PM��
=PM��
��PM=PN= ![]() ʱ��
ʱ��
��xP=3�� ![]() =��
=�� ![]() ��yP=��
��yP=�� ![]() ��
�� ![]() +4=
+4= ![]() ��
��
��P���� ![]() ��
�� ![]() ����
����
��ֱ��PM����ʽΪy=�� ![]() x+
x+ ![]() ��
��
�� 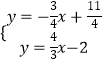 �����
����� 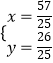 ��
��
���M�� ![]() ��
�� ![]() ��
��
��EM= ![]() =
= ![]() ��
��
��NP=NMʱ����ֱ��EF��Գ��ύ�ڵ�K��K��3��2����
��ʱ��N��PM�Ĵ�ֱƽ�����ϣ�DN=NK��
��N��3��5����P�� ![]() ��5����
��5����
��ֱ��PM�Ľ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
�� 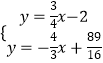 ���
��� 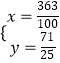 ��
��
��M�� ![]() ��
�� ![]() ����
����
��EM= ![]() =
= ![]() ��
��
��PM=MNʱ��cos��MPN= ![]() =
= ![]() ��
��
��PN= ![]() ���ɴ˿ɵ�P����
���ɴ˿ɵ�P���� ![]() ��
�� ![]() ����
����
��ֱ��PM����ʽΪy=�� ![]() x��
x�� ![]() ��
��
�� 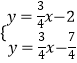 ���
��� 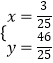 ��
��
��M�� ![]() ����
���� ![]() ����
����
��EM= ![]() =
= ![]() ��
��
����������EM= ![]() ��
�� ![]() ��
�� ![]() ��
��
����������1�����Լ��������߽���ʽΪy=�� ![]() ��x+3����x��9����չ�����ɣ���2����PH��AQ��H����AH=HQ=
��x+3����x��9����չ�����ɣ���2����PH��AQ��H����AH=HQ= ![]() ����ͼ1�У�������S=S��ADQ��S��APQ�������κ��������ö��κ��������ʼ��ɽ�����⣮��3���������������ۢ�PM=PN����NP=NM����MN=MP���ֱ����ֱ��PM�Ľ���ʽ�����÷����������M���꼴�ɽ�����⣮
����ͼ1�У�������S=S��ADQ��S��APQ�������κ��������ö��κ��������ʼ��ɽ�����⣮��3���������������ۢ�PM=PN����NP=NM����MN=MP���ֱ����ֱ��PM�Ľ���ʽ�����÷����������M���꼴�ɽ�����⣮
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�