题目内容
【题目】甲乙两人进行射击训练，两人分别射击12次，如图分别统计了两人的射击成绩，已知甲射击成绩的方差S甲2= 
，平均成绩 
=8.5．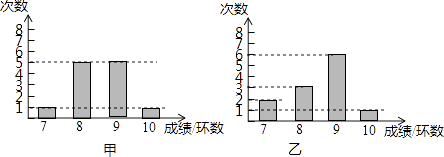 
（1）根据图上信息，估计乙射击成绩不少于9环的概率是多少？
（2）求乙射击的平均成绩的方差，并据此比较甲乙的射击“水平”．
S2= 
[（x1﹣ 
）2+（x2﹣ ）2…（xn﹣ ）2]．
【答案】
（1）解：∵由图可知，乙射击的总次数是12次，不少于9环的有7次，
∴乙射击成绩不少于9环的概率= 
（2）解： 
= 
=8.5（环），
= 
[（7﹣8.5）2×2+（8﹣8.5）2×3+（9﹣8.5）2×6+（10﹣8.5）2]
= 
= 
．
∵ 
= ， 
＜ ，
∴甲的射击成绩更稳定
【解析】本题考查的是概率公式，熟记随机事件的概率公式及方差的定义是解答此题的关键．（1）根据条形统计图求出乙的射击总数与不少于9环的次数，根据概率公式即可得出结论；（2）求出乙的平均成绩及方差，再与甲的平均成绩及方差进行比较即可．
【考点精析】根据题目的已知条件，利用概率公式的相关知识可以得到问题的答案，需要掌握一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n．
练习册系列答案
相关题目
