Question

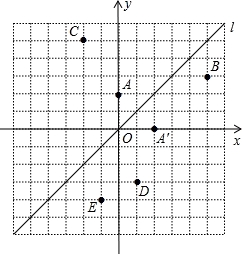
如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．

实验与探究：

（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（﹣2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′__________、C′__________；

归纳与发现：

（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为__________（不必证明）；

运用与拓广：

（3）已知两点D（1，﹣3）、E（﹣1，﹣4），试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．

Answer 1

【考点】一次函数综合题．

【专题】综合题．

【分析】易找到点B关于第一、三象限角平分线的对称点B′的坐标为（3，5），再结合已知的点A的坐标，我们不难猜想点C′坐标是（5，﹣2），然后找到点C′，可以发现CC′被第一、三象限角平分线垂直且平分，由此可以推想到坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为（b，a），即它们纵、横坐标互换位置．

【解答】解：（1）如图：B′（3，5），C′（5，﹣2）；

（2）（b，a）；

（3）由（2）得，D（1，﹣3）关于直线l的对称点D′的坐标为（﹣3，1），连接D′E交直线l于点Q，此时点Q到D、E两点的距离之和最小．

设过D′（﹣3，1）、E（﹣1，﹣4）直线的解析式为y=kx+b，

则

∴

∴直线D′E的解析式为：y=﹣x﹣

由

得

∴所求Q点的坐标为（，）．

【点评】本题的解答经历了实验﹣﹣猜想﹣﹣验证﹣﹣推广的思维过程，这也是我们认识事物规律的一般方法，主要考查一次函数的性质和图象，中等难度．