题目内容
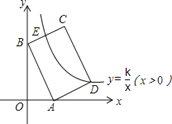
【题目】如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为_____.
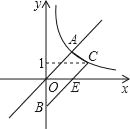
【答案】2![]() +10.
+10.
【解析】因为AO∥BC,上底边OA在直线y=x上,
则可设BC的解析式为y=x+b,
将B(0,﹣4)代入上式得,b=﹣4,
BC的解析式为y=x﹣4.
把y=1代入y=x﹣4,得x=5,C点坐标为(5,1),
则反比例函数解析式为y=![]() ,
,
将它与y=x组成方程组得:![]() ,
,
解得x=![]() ,x=﹣
,x=﹣![]() (负值舍去).
(负值舍去).
代入y=x得,y=![]() ,
,
A点坐标为(![]() ,
,![]() ),
),
OA=![]() =
=![]() ,
,
BC=![]() =5
=5![]() ,
,
∵BC的解析式为y=x﹣4,
∴E(4,0),
∵B(0,﹣4),
∴BE=![]() =4
=4![]() ,
,
设BE边上的高为h,
![]() h×
h×![]() =4×4×
=4×4×![]() ,
,
解得:h=2![]() ,
,
则梯形AOBC高为:2![]() ,
,
梯形AOBC面积为:![]() ×2
×2![]() ×(
×(![]() +5
+5![]() )=2
)=2![]() +10,
+10,
故答案为:2![]() +10.
+10.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目