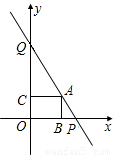题目内容
 如图,直线y=x与反比例函数y=
如图,直线y=x与反比例函数y=| k |
| x |
| k |
| x |
(1)若点B的坐标为(0,4),求k的值;
(2)在(1)的条件下,求证:HG=HE.
分析:(1)利用点B的坐标为(0,4)易得点A的坐标为(4,4),然后把点A的坐标代入y=
即可求出k的值;
(2)设H点坐标为(a,0),易得C点坐标为(a,4),G点坐标为(a,
),则GH=
,利用等角的余角相等得到∠OCH=∠CEH,根据相似三角形的判定得Rt△OCH∽Rt△CEH,则OH:CH=CH:EH,然后把OH=a,CH=4代入得到EH=
,于是有HG=HE.
| k |
| x |
(2)设H点坐标为(a,0),易得C点坐标为(a,4),G点坐标为(a,
| 16 |
| a |
| 16 |
| a |
| 16 |
| a |
解答:(1)解:∵点B的坐标为(0,4),AB⊥y轴,
∴点A的纵坐标为4,
∵点A在直线y=x上,
∴点A的坐标为(4,4),
把A(4,4)代入y=
得k=4×4=16;
(2)证明:反比例函数的解析式为y=
,
设H点坐标为(a,0),
∵CH⊥x轴,
∴C点坐标为(a,4),G点坐标为(a,
),
∴GH=
,
∵∠CHO=∠OCE=90°,
∴∠OHC-∠HOC=∠OCE-∠EOC,即∠OCH=∠CEH,
∴Rt△OCH∽Rt△CEH,
∴OH:CH=CH:EH,
∴EH=
,
∵OH=a,CH=4,
∴EH=
,
∴HG=HE.
∴点A的纵坐标为4,
∵点A在直线y=x上,
∴点A的坐标为(4,4),
把A(4,4)代入y=
| k |
| x |
(2)证明:反比例函数的解析式为y=
| 16 |
| x |
设H点坐标为(a,0),
∵CH⊥x轴,
∴C点坐标为(a,4),G点坐标为(a,
| 16 |
| a |
∴GH=
| 16 |
| a |
∵∠CHO=∠OCE=90°,
∴∠OHC-∠HOC=∠OCE-∠EOC,即∠OCH=∠CEH,
∴Rt△OCH∽Rt△CEH,
∴OH:CH=CH:EH,
∴EH=
| CH2 |
| OH |
∵OH=a,CH=4,
∴EH=
| 16 |
| a |
∴HG=HE.
点评:本题考查了反比例函数综合题:反比例函数图象上的点的坐标满足其函数解析式;常用待定系数法求函数的解析式;正确运用三角形相似的判定与性质进行几何计算.

练习册系列答案
相关题目
 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.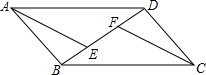 如图:四边形ABCD中AB=DC,AD=BC,点E、F在线段BD上,且BE=DF.(1)求证:△ABD≌△CDB;
如图:四边形ABCD中AB=DC,AD=BC,点E、F在线段BD上,且BE=DF.(1)求证:△ABD≌△CDB;