Question

10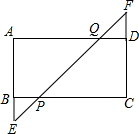．如图，矩形ABCD中，延长AB至E，延长CD至F，BE=DF，连接EF，与BC、AD分别相交于P、Q两点．
（1）求证：CP=AQ；
（2）若BP=1，PQ=2$\sqrt{2}$，∠AEF=45°，求矩形ABCD的面积．

Answer 1

分析 （1）由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°，AB=CD，AD=BC，AB∥CD，AD∥BC，证出∠E=∠F，AE=CF，由ASA证明△CFP≌△AEQ，即可得出结论；
（2）证明△BEP、△AEQ是等腰直角三角形，得出BE=BP=1，AQ=AE，求出PE=$\sqrt{2}$BP=$\sqrt{2}$，得出EQ=PE+PQ=3$\sqrt{2}$，由等腰直角三角形的性质和勾股定理得出AQ=AE=3，求出AB=AE-BE=2，DQ=BP=1，得出AD=AQ+DQ=4，即可求出矩形ABCD的面积．

解答 （1）证明：∵四边形ABCD是矩形，
∴∠A=∠ABC=∠C=∠ADC=90°，AB=CD，AD=BC，AB∥CD，AD∥BC，
∴∠E=∠F，
∵BE=DF，
∴AE=CF，
在△CFP和△AEQ中，$\left\{\begin{array}{l}{∠C=∠A}&{\;}\\{CF=AE}&{\;}\\{∠F=∠E}&{\;}\end{array}\right.$，
∴△CFP≌△AEQ（ASA），
∴CP=AQ；
（2）解：∵AD∥BC，
∴∠PBE=∠A=90°，
∵∠AEF=45°，
∴△BEP、△AEQ是等腰直角三角形，
∴BE=BP=1，AQ=AE，
∴PE=$\sqrt{2}$BP=$\sqrt{2}$，
∴EQ=PE+PQ=$\sqrt{2}$+2$\sqrt{2}$=3$\sqrt{2}$，
∴AQ=AE=3，
∴AB=AE-BE=2，
∵CP=AQ，AD=BC，
∴DQ=BP=1，
∴AD=AQ+DQ=3+1=4，
∴矩形ABCD的面积=AB•AD=2×4=8．

点评 本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识；熟练掌握矩形的性质，证明三角形全等是解决问题的关键．