题目内容
如图，△ABC的三边长为5，12，13．设其三条高的交点为H，外心为O，求OH．
考点：勾股定理的逆定理,三角形的外接圆与外心
专题：
分析：根据勾股定理的逆定理得此三角形是直角三角形，则其外心就是斜边的中点；又因为高的交点是直角顶点，则OH就是斜边上的中线，等于斜边的一半是
．
| 13 |
| 2 |
解答：
解：∵△ABC的三边为5，12，13，
∴△ABC是直角三角形，
∴OH=13×
=
．
解：∵△ABC的三边为5，12，13，∴△ABC是直角三角形，
∴OH=13×
| 1 |
| 2 |
| 13 |
| 2 |
点评：考查了勾股定理的逆定理，此题首先能够判定它是一个直角三角形，然后确定它的外心就是斜边的中点，高的交点就是直角顶点；从而根据直角三角形斜边上的中线等于斜边的一半求解．
练习册系列答案
相关题目
下列各式中不能用完全平方公式分解的是（ ）
| A、-x2+2xy-y2 |
| B、x4-2x3y+x2y2 |
| C、m2-m+0.25 |
| D、x2-xy+y2 |
若x2m-1y与x5ym+n是同类项，那么（mn+5）2008=（ ）
| A、1 | B、-1 |
| C、1或-1 | D、无法确定 |
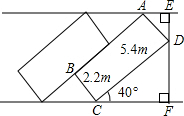随着人民生活水平的提高，小轿车也逐渐进入千家万户．为了解决停车难问题，我县交警大队在城区划定了许多机动车停车位．如图，矩形ABCD的供一辆机动车停放的车尾示意图，已知BC=2.2m，∠DCF=40°，请计算车位所占街道的宽度EF．（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果精确到0.1m）