题目内容
如图,点A、B、C、D在⊙O上,∠ADC=60°,C是弧AB的中点.
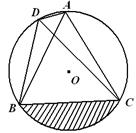
(1)判断△ABC的形状,并说明理由;
(2)若BC=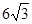 cm,求图中阴影部分的面积.
cm,求图中阴影部分的面积.

(1)判断△ABC的形状,并说明理由;
(2)若BC=
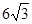 cm,求图中阴影部分的面积.
cm,求图中阴影部分的面积.(1)△ABC是等边三角形;(2)(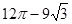 )平方厘米
)平方厘米
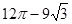 )平方厘米
)平方厘米试题分析:(1)由C是弧AB的中点可得弧AC=弧BC,根据圆周角定理可得∠ADC=∠ABC=∠BAC=∠BDC=60°,即可得到△ABC的形状;
(2)连接BO、OC,过O作OE⊥BC于E,先根据垂径定理求得BE=EC=
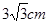 ,再根据圆周角定理可得∠BOC、∠BOE的度数,在Rt△BOE中,根据∠BOE的正弦函数可求得OB的长,再根据扇形的面积公式及三角形的面积公式求解即可.
,再根据圆周角定理可得∠BOC、∠BOE的度数,在Rt△BOE中,根据∠BOE的正弦函数可求得OB的长,再根据扇形的面积公式及三角形的面积公式求解即可.(1)∵C是弧AB的中点,
∴弧AC=弧BC,
∴∠ADC=∠ABC=∠BAC=∠BDC=60°
∴∠ACB=60°,
∴AC=AB=BC,
∴△ABC是等边三角形;
(2)连接BO、OC,过O作OE⊥BC于E
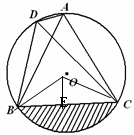
∵BC=
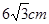 ,
,∴BE=EC=
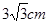 ,
,∵∠BAC=60°,
∴∠BOC=120°,
∴∠BOE=60°,在Rt△BOE中,sin60°=
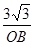 ,
,∴OB=6cm,
∴S扇形BOC=
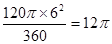 cm2
cm2∵S△BOC=
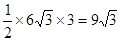 cm2
cm2 ∴S阴影 =
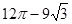 cm2
cm2 答:图中阴影部分的面积是(
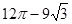 )平方厘米
)平方厘米点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 是过格点A,B,C的圆弧,请完成下列问题:
是过格点A,B,C的圆弧,请完成下列问题:
 (1)用无刻度的直尺,过点B作与
(1)用无刻度的直尺,过点B作与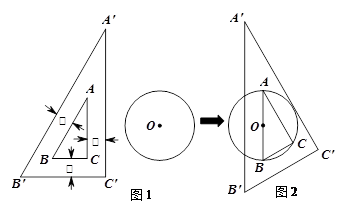
 BB′C′+
BB′C′+
 ,求
,求 的长度(结果保留π).
的长度(结果保留π). 和
和 度数分别为36°和108°,弦CD与弦AB长度的差为 (用含有R的代数式表示).
度数分别为36°和108°,弦CD与弦AB长度的差为 (用含有R的代数式表示).
 ,⊙O2的半径是
,⊙O2的半径是 ,若这两圆相交,则它们的圆心距
,若这两圆相交,则它们的圆心距 的取值范围在数轴上表示为
的取值范围在数轴上表示为
 内接于⊙
内接于⊙ , 若
, 若 , 则
, 则 ( )
( )



