题目内容
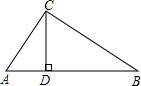 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积.
分析:(1)根据直角三角形面积的求法,即可得出△ABC的面积,再根据三角形的面积公式即可求得CD的长,
(2)取AC得中点E,连接BE,根据中线的性质可得出△ABE和△BCE的面积相等,从而得出答案.
(2)取AC得中点E,连接BE,根据中线的性质可得出△ABE和△BCE的面积相等,从而得出答案.
解答:解:∵∠ACB=90°,BC=12cm,AC=5cm,
∴AB=
=13cm,
∵S△ABC=BC×AC=30cm2,
∴
AB•CD=30,
∴CD=
cm;
(2)如图所示:
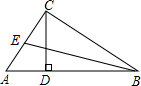
∵E为AC的中点,
∴S△ABE=
S△ABC=
×30=15cm2.
∴AB=
| AC2+BC2 |
∵S△ABC=BC×AC=30cm2,
∴
| 1 |
| 2 |
∴CD=
| 60 |
| 13 |
(2)如图所示:

∵E为AC的中点,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了勾股定理的逆定理、直角三角形的面积的计算方法及面积公式应用同时考查了直角三角形的高、中点的性质,难度适中.

练习册系列答案
相关题目
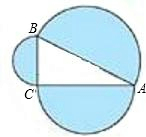 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
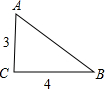
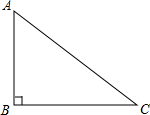 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.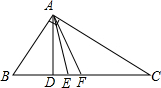 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=