Question

【题目】如图-1，△ABC和△DEC都是等腰直角三角形，∠ACB=∠DCE=90°，E在线段AC上，连接AD，BE的延长线交AD于F．

（1）猜想线段BE，AD的数量关系和位置关系：________________________（不必证明）；

（2）当点E为△ABC内部一点时，使点D和点E分别在AC的两侧，其它条件不变．

① 请你在图-2中补全图形；

②（1）中结论成立吗？若成立，请证明；若不成立，请说明理由．

Answer 1

【答案】（1）BE=AD ；BE⊥AD；（2）①答案见解析；②成立

【解析】（1）先通过SAS证△BCE和△ACD全等，再根据全等三角形的性质即可得出BE，AD的数量关系和位置关系；

（2）按要求画图所，按（1）的证明思路即可进行证明.

解：（1）∵△ABC和△DEC都是等腰直角三角形，且∠ACB=∠DCE=90°，

∴BC=AC,CE=CD,

∴△BCE≌△ACD(SAS),

∴BE=AD ,

∵

∴

∴BE⊥AD.

故答案为：BE=AD ,BE⊥AD.

（2）①如图

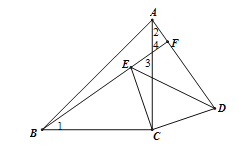
②（1）中结论仍然成立．

证明：∵△ABC和△DEC都是等腰直角三角形，∠ACB=∠DCE=90°，

∴BC=AC，EC=DC，

∵∠ACB=∠DCE=90°，

∴∠ACB =∠DCE ，

∴∠BCE=∠ACD，

在△BCE和△ACD中，

∵BC=AC，∠BCE=∠ACD，EC=DC，

∴△BCE≌△ACD（SAS），

∴ BE=AD，∠1=∠2，

∵∠3=∠4，

∴∠AFB=∠ACB=90°，

∴BE⊥AD.