题目内容
如图所示：△ABC中，∠C=90°，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且CD=6cm，则DE的长为
- A.4cm
- B.6cm
- C.8cm
- D.10cm
B
分析：根据角平分线上的点到角的两边的距离相等的性质即可得解．
解答：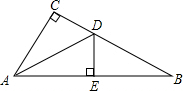
解：∵AD平分∠CAB，∠C=90°，
∴DE=CD，
∵CD=6cm，
∴DE=6cm．
故选B．
点评：本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．
分析：根据角平分线上的点到角的两边的距离相等的性质即可得解．
解答：
解：∵AD平分∠CAB，∠C=90°，∴DE=CD，
∵CD=6cm，
∴DE=6cm．
故选B．
点评：本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
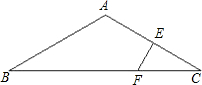如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=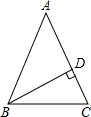
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．