题目内容
P是正方形ABCD所在平面内一点,PB= ,PC=1,∠BPC=135°,则AP的长为 .
,PC=1,∠BPC=135°,则AP的长为 .
【答案】分析:先根据图形旋转的性质得出△BPQ是等腰直角三角形,故可判断△PCQ是直角三角形,再根据勾股定理即可得出结论.
解答: 解:把△ABP绕点B顺时针旋转90°,到达△CBQ位置,
解:把△ABP绕点B顺时针旋转90°,到达△CBQ位置,
∵△CBQ是△ABP旋转而成90°,
∴PB=BQ,∠PBQ=90°,
∴△BPQ是等腰直角三角形,
∵PB= ,
,
∴PQ= =2,∠BPQ=45°,
=2,∠BPQ=45°,
∴∠CPQ=135°-45°=90°
∴△PCQ是直角三角形,
∴AP=CQ= =
= =
= .
.
故答案为: .
.
点评:本题考查的是图形旋转的性质及勾股定理,熟知图形旋转前、后的图形全等是解答此题的关键.
解答:
 解:把△ABP绕点B顺时针旋转90°,到达△CBQ位置,
解:把△ABP绕点B顺时针旋转90°,到达△CBQ位置,∵△CBQ是△ABP旋转而成90°,
∴PB=BQ,∠PBQ=90°,
∴△BPQ是等腰直角三角形,
∵PB=
 ,
,∴PQ=
 =2,∠BPQ=45°,
=2,∠BPQ=45°,∴∠CPQ=135°-45°=90°
∴△PCQ是直角三角形,
∴AP=CQ=
 =
= =
= .
.故答案为:
 .
.点评:本题考查的是图形旋转的性质及勾股定理,熟知图形旋转前、后的图形全等是解答此题的关键.

练习册系列答案
相关题目
 26、已知:如图所示,E是正方形ABCD边BC延长线一点,若EC=AC,AE交CD于F,则∠AFC=
26、已知:如图所示,E是正方形ABCD边BC延长线一点,若EC=AC,AE交CD于F,则∠AFC=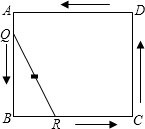 如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积记为S.点N是正方形ABCD内任一点,把N点到四个顶点A,B,C,D的距离均不小于1的概率记为P,则S=( )
如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积记为S.点N是正方形ABCD内任一点,把N点到四个顶点A,B,C,D的距离均不小于1的概率记为P,则S=( )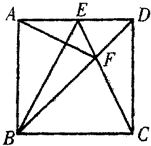 23、如图所示,E是正方形ABCD中AD边上的中点,BD与CE交于点F.请你根据图形判断AF与BE的位置具有什么关系?并给予证明.
23、如图所示,E是正方形ABCD中AD边上的中点,BD与CE交于点F.请你根据图形判断AF与BE的位置具有什么关系?并给予证明.
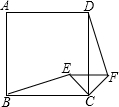 如图所示,点E是正方形ABCD内任一点,把△BEC绕点C旋转至△DFC的位置,∠CFE=
如图所示,点E是正方形ABCD内任一点,把△BEC绕点C旋转至△DFC的位置,∠CFE=