题目内容
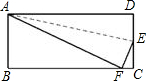
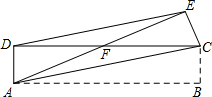
如图，四边形ABCD是矩形，AB=12，AD=5，把矩形沿直线AC折叠，点B落在点E处，连接DE，则DE：AC的值是（ ）
| A．2：3 | B．119：169 | C．23：27 | D．12：13 |
从D，E处向AC作高DM，EN，
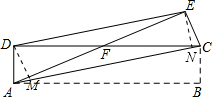
∵AB=12，AD=5，则AC=13，
由△AEC的面积=
×EC×AE=30，得EN=
，
根据勾股定理得CN=
=
，同理AM=
．
所以DE=13-
=
，
所以DE：AC=119：169．
故选B．
∵AB=12，AD=5，则AC=13，
由△AEC的面积=
| 1 |
| 2 |
| 60 |
| 13 |
根据勾股定理得CN=
| EC2-EN2 |
| 25 |
| 13 |
| 25 |
| 13 |
所以DE=13-
| 50 |
| 13 |
| 119 |
| 13 |
所以DE：AC=119：169．
故选B．
练习册系列答案
相关题目
