题目内容
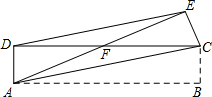
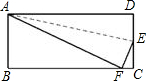
如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且量得BF=12cm.
求:(1)AD的长;(2)DE的长.
求:(1)AD的长;(2)DE的长.

(1)∵∠B=90°,
∴AF=
=13(cm). (1分)
∵∠C=90°,AD、AF关于AE轴对称,
∴AD=AF=13cm. (2分)
(2)由已知及对称性可得
BC=AD=13cm,CD=AB=5cm,DE=EF.
∴CF=BC-BF=1cm. (3分)
设DE=EF=xcm,则CE=(5-x)cm,(4分)
由勾股定理得:CE2+CF2=EF2
∴(5-x)2+12=x2(5分)
解得x=2.6. (6分)
∴DE=2.6cm. (7分)
∴AF=
| AB2+BF2 |
∵∠C=90°,AD、AF关于AE轴对称,
∴AD=AF=13cm. (2分)
(2)由已知及对称性可得
BC=AD=13cm,CD=AB=5cm,DE=EF.
∴CF=BC-BF=1cm. (3分)
设DE=EF=xcm,则CE=(5-x)cm,(4分)
由勾股定理得:CE2+CF2=EF2
∴(5-x)2+12=x2(5分)
解得x=2.6. (6分)
∴DE=2.6cm. (7分)

练习册系列答案
相关题目