题目内容
3．计算：（1）$\frac{a-1}{{a}^{2}-4a+4}$÷$\frac{{a}^{2}-1}{{a}^{2}-4}$．
（2）$\frac{{a}^{2}}{a-1}$-a-1．
分析 （1）原式通分并利用同分母分式的加法法则计算即可得到结果；
（2）原式通分并利用同分母分式的减法法则计算即可得到结果．
解答 解：（1）原式=$\frac{a-1}{（a-2）^{2}}$÷$\frac{（a+1）（a-1）}{（a+2）（a-2）}$=$\frac{a-1}{（a-2）^{2}}$•$\frac{（a+2）（a-2）}{（a+1）（a-1）}$=$\frac{a+2}{（a+1）（a-2）}$；
（2）原式=$\frac{{a}^{2}-（a+1）（a-1）}{a-1}$=$\frac{{a}^{2}-{a}^{2}+1}{a-1}$=$\frac{1}{a-1}$．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
13．
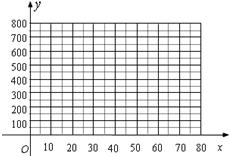2015年9月19日第九届合肥文博会开幕．开幕前夕，我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：
（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？
（3）开幕后，合肥市物价部门规定，该工艺品销售单价最高不能超过38元/件，那么销售单价定为多少时，工艺厂销售该工艺品每天获得的利润最大？最大利润是多少？
2015年9月19日第九届合肥文博会开幕．开幕前夕，我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：| 销售单价x（元/件） | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量（y件） | … | 500 | 400 | 300 | 200 | 100 | … |
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？
（3）开幕后，合肥市物价部门规定，该工艺品销售单价最高不能超过38元/件，那么销售单价定为多少时，工艺厂销售该工艺品每天获得的利润最大？最大利润是多少？
问题探究：观察下面由“※”组成的图案和算式，解答问题：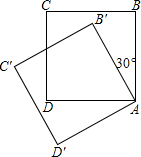
如图，把边长为4的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于$\frac{16\sqrt{3}}{3}$．
15．若|x-$\frac{1}{2}$|与（y+1）2互为相反数，则x2+y3的值是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | -$\frac{1}{4}$ | D． | -$\frac{3}{4}$ |
如图，已知△ABC各顶点的坐标分别为A（-3，2），请你画出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1的各顶点坐标．