题目内容
 如图,数轴上的点A所表示的数为k,化简|k|+|1-k|的结果为
如图,数轴上的点A所表示的数为k,化简|k|+|1-k|的结果为考点:数轴,绝对值
专题:
分析:由数轴可知:k>1,所以可知:k>0,1-k<0.计算绝对值再化简即可.
解答:解:∵由数轴可知:k>1,
∴k>0,1-k<0.
∴|k|+|1-k|=k-1+k=2k-1.
故答案为:2k-1.
∴k>0,1-k<0.
∴|k|+|1-k|=k-1+k=2k-1.
故答案为:2k-1.
点评:此题主要考查了绝对值的性质,即正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值还是0.除此之外还考查了数轴的概念和整式的加减.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
已知A(x1,y1),B(x2,y2)是反比例函数y=
在平面直角坐标系xOy的第一象限上图象上的两点,满足y1+y2=
,x2-x1=
,则S△AOB=( )
| 1 |
| x |
| 7 |
| 2 |
| 5 |
| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
 如图,数轴上P表示的数可能是( )
如图,数轴上P表示的数可能是( )| A、-2.67 | B、-3.48 |
| C、3.25 | D、-1.99 |
小明要用纸板制作一个高为3cm,底面周长是8πcm的圆锥形漏斗模型,若不计接缝和损耗,则他所需的纸板面积是( )
| A、12πcm2 |
| B、15πcm2 |
| C、18πcm2 |
| D、20πcm2 |
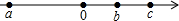
 如图,在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上的一点,ED=CD,连接EC,求证:EA=EC.
如图,在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上的一点,ED=CD,连接EC,求证:EA=EC. 已知函数图象如图所示,根据图象可得:
已知函数图象如图所示,根据图象可得: