题目内容
如图，已知三角形ABC与三角形DEF是全等形，则相等的线段有
- A.1组
- B.2组
- C.3组
- D.4组
D
分析：根据全等三角形的对应边相等，即可得到三组相等的线段，再根据BC=EF，即可得到BE=CF．
解答：∵三角形ABC与三角形DEF是全等形，
∴AB=DE，AC=DF，BC=EF，
∵BC=EF即BE+EC=CF+EC
∴BE=CF
∴共有AB=DE，AC=DF，BC=EF，BE=CF4组．
故选D．
点评：本题主要考查了全等三角形的性质，全等三角形的对应边相等．
分析：根据全等三角形的对应边相等，即可得到三组相等的线段，再根据BC=EF，即可得到BE=CF．
解答：∵三角形ABC与三角形DEF是全等形，
∴AB=DE，AC=DF，BC=EF，
∵BC=EF即BE+EC=CF+EC
∴BE=CF
∴共有AB=DE，AC=DF，BC=EF，BE=CF4组．
故选D．
点评：本题主要考查了全等三角形的性质，全等三角形的对应边相等．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
15、如图，已知CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于点O，且AO平分∠BAC，那么图中全等三角形共有（ ）对．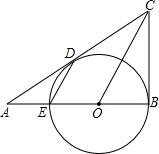
点E，与AC切于点D．
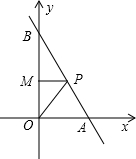）是折线O→A→B上的动点（不与O点、B点重合），连接OP，MP，设△OPM的面积为S．
按要求画图并填空：如图，已知三角形ABC及点D，CB⊥AB，B为垂足．