题目内容
如图，已知直线AB与x轴交于A（6，0）点，与y轴交于B（0，10）点，点M的坐标为（0，4），点P（x，y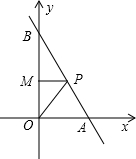
）是折线O→A→B上的动点（不与O点、B点重合），连接OP，MP，设△OPM的面积为S．（1）求S关于x的函数表达式，并求出x的取值范围；
（2）当△OPM是以OM为底边的等腰三角形时，求S的值．
分析：（1）△OPM的面积为S=
OM•P点的横坐标；
（2）当△OPM是以OM为底边的等腰三角形时，P在线段OM的垂直平分线上，则P点的纵坐标是2．即可求解．
| 1 |
| 2 |
（2）当△OPM是以OM为底边的等腰三角形时，P在线段OM的垂直平分线上，则P点的纵坐标是2．即可求解．
解答：解：（1）∵△OPM的面积为S=
OM•x，
∴S=2x（0＜x≤6）（3分）
（2）由题意得：
∵点M的坐标为（0，4），
∴三角形OPM的顶点P的纵坐标为：2，
直线AB的解析式为：y=-
x+10
把P点的纵坐标代入上，把P点的纵坐标代入上得x=
，S=
（8分）
| 1 |
| 2 |
∴S=2x（0＜x≤6）（3分）
（2）由题意得：
∵点M的坐标为（0，4），
∴三角形OPM的顶点P的纵坐标为：2，
直线AB的解析式为：y=-
| 5 |
| 3 |
把P点的纵坐标代入上，把P点的纵坐标代入上得x=
| 24 |
| 5 |
| 48 |
| 5 |
点评：本题是等腰三角形的知识与函数相结合的问题，正确表示出三角形的面积是解决本题的关键．
练习册系列答案
相关题目
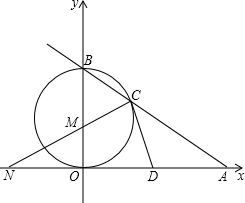方程x2-mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM．
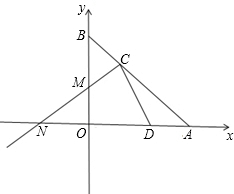如图，已知直线AB与x轴、y轴分别交于A和B，OA=4，且OA、OB长是关于x的方程x2-mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM并延长交x轴于N．
26、如图，已知直线AB与CD相交于点O，OB平分∠EOD，∠1+∠2=90°，
A=3，点C的横坐标为-3，tan∠BAO=
如图，已知直线AB与CD相交于点O，OE⊥CD，OF平分∠BOE，若∠AOC=∠EOF，