题目内容
1.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )| A. | 选①② | B. | 选①③ | C. | 选②④ | D. | 选②③ |
分析 根据要判定四边形是正方形,则需能判定它既是菱形又是矩形进而分别分析得出即可.
解答 解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,
所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意.
故选:D.
点评 本题考查了正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个矩形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.

练习册系列答案
相关题目
12. 如图,AB∥CD,若∠1=45°,则∠2的度数是( )
如图,AB∥CD,若∠1=45°,则∠2的度数是( )
 如图,AB∥CD,若∠1=45°,则∠2的度数是( )
如图,AB∥CD,若∠1=45°,则∠2的度数是( )| A. | 135° | B. | 90° | C. | 45° | D. | 30° |
6.下列方程有实数根的有( )
①x2+x+4=0;②x2+4x+4=0;③x2+4x-2=0.
①x2+x+4=0;②x2+4x+4=0;③x2+4x-2=0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
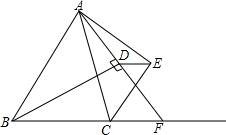 已知:如图,BD为△ABC的内角平分线,CE为△ABC的外角平分线,AD⊥BD于D,AE⊥CE于E,延长AD交BC的延长线于F,连接DE,设BC=a,AC=b,AB=c,(a<b<c)给出以下结论正确的有①③.
已知:如图,BD为△ABC的内角平分线,CE为△ABC的外角平分线,AD⊥BD于D,AE⊥CE于E,延长AD交BC的延长线于F,连接DE,设BC=a,AC=b,AB=c,(a<b<c)给出以下结论正确的有①③.