题目内容
(9分)如图1,△ABC中,AB=AC=5cm,BC=6cm,边长为2cm的菱形DEFG两边DG、DE分别在AC、AB上.若菱形DEFG以1cm/s的速度沿射线AC方向平移.(1)经过 ▲ 秒菱形DEFG的顶点F恰好在BC上;
(2)求菱形DEFG的面积;
(3)设菱形DEFG与△ABC的重合部分为Scm2,菱形DEFG平移的时间为t秒.求S与t的函数关系式.

解:(1)1.…………………………2分
(2)方法一:
如图,连接GE、AF,交于点O,并延长AF 交BC于点H.

∵由AG=AE得∠AGE=∠AEG,由AB=AC得∠B=∠C,
 ②当1<t≤3时,
②当1<t≤3时,


AD=t,则CE=5–t–2=3–t,EN=EC=3–t,
故FN=2–(3–t)="t–1" .
 ③当3<x≤5时,AD=t,则CD=5–t,解析:
③当3<x≤5时,AD=t,则CD=5–t,解析:
src="https://thumb.zyjl.cn/pic1/imagenew2/czsx/18/71638.jpg" >【解析】略
(2)方法一:
如图,连接GE、AF,交于点O,并延长AF 交BC于点H.

∵由AG=AE得∠AGE=∠AEG,由AB=AC得∠B=∠C,
 ②当1<t≤3时,
②当1<t≤3时,

AD=t,则CE=5–t–2=3–t,EN=EC=3–t,
故FN=2–(3–t)="t–1" .
 ③当3<x≤5时,AD=t,则CD=5–t,解析:
③当3<x≤5时,AD=t,则CD=5–t,解析:src="https://thumb.zyjl.cn/pic1/imagenew2/czsx/18/71638.jpg" >【解析】略

练习册系列答案
相关题目
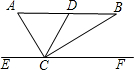 如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )
如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )| A、35° | B、45° | C、55° | D、65° |
 17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:
17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: 8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )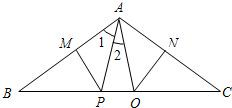 如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.
如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数. 19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.
19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.