题目内容
Rt△ABC中,∠ACB=90°,BC=15,AC=20.CD为斜边AB上的高.矩形EFGH的边EF与CD重合,A、D、B、G在同一直线上(如图1).将矩形EFGH向左边平移,EF交AC于M(M不与A重合,如图2),连接BM,BM交CD于N,连接NF.(1)直接写出图2中所有与△CDB相似的三角形;
(2)设CE=x,△MNF的面积为y,求y与x的函数关系式,写出自变量x的取值范围,并求△MNF的最大面积;
(3)在平移过程中是否存在四边形MFNC为平行四边形的情形?若存在,求出x的值;若不存在,说明理由.
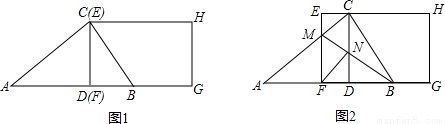
【答案】分析:(1)有△CEM∽△CDB,△AFM∽△CDB,△ADC∽△CDB,△ACB∽△CDB;
(2)过N作NQ⊥EF于Q,求出EC=DF=NQ=x,由勾股定理求出AB=25,根据三角形面积公式求出CD=12,由勾股定理求出AD=16,BD=9,根据△AMF∽△ACD求出FM=- x+12,代入y=
x+12,代入y= FM×NQ求出即可;
FM×NQ求出即可;
(3)根据△BDN∽△BFM求出DN= (-
(- x+12),求出CN=12-
x+12),求出CN=12-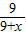 (-
(- x+12),根据平行四边形的性质得出方程-
x+12),根据平行四边形的性质得出方程- x+12=12-
x+12=12-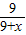 (-
(- x+12),求出方程的解即可.
x+12),求出方程的解即可.
解答:解:(1)△CEM∽△CDB,△AFM∽△CDB,△ADC∽△CDB,△ACB∽△CDB;
(2)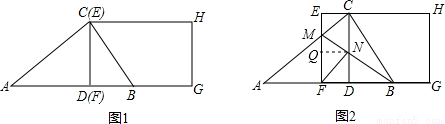
过N作NQ⊥EF于Q,如图2,
∵据平移和矩形性质得出EF∥CD,EC∥FD,
∴四边形EFDC是矩形,
∴EC=DF=NQ=x,
∵△ACB中,∠ACB=90°,BC=15,AC=20,由勾股定理得:AB=25,
S△ACB= AB×CD=
AB×CD= AC×BC,
AC×BC,
∴CD=12,由勾股定理得:AD=16,BD=9,
∵EF∥DC,
∴△AMF∽△ACD,
∴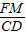 =
=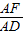 ,
,
∴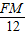 =
=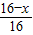 ,
,
FM=- x+12,
x+12,
∴y= FM×NQ=
FM×NQ= (-
(- x+12)x,
x+12)x,
y=- x2+6x,
x2+6x,
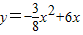 ,
,
y=- (x-8)2+24,
(x-8)2+24,
即当x=8时,△MNF的最大面积是24;
自变量x的取值范围是0<x<16,当x=8时,有最大值24;
(3)∵EF∥CD,
∴△BDN∽△BFM,
∴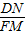 =
=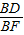 ,
,
∴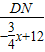 =
=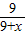 ,
,
∴DN=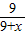 (-
(- x+12),
x+12),
∴CN=12-DN=12-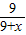 (-
(- x+12),
x+12),
假设存在四边形MFNC为平行四边形,
此时CN=FM,
即- x+12=12-
x+12=12-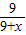 (-
(- x+12),
x+12),
解得:x=6,
即在平移过程中存在四边形MFNC为平行四边形的情形,此时x的值是6.
点评:本题考查了相似三角形的性质和判定,矩形的性质和判定,平行四边形性质,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.
(2)过N作NQ⊥EF于Q,求出EC=DF=NQ=x,由勾股定理求出AB=25,根据三角形面积公式求出CD=12,由勾股定理求出AD=16,BD=9,根据△AMF∽△ACD求出FM=-
 x+12,代入y=
x+12,代入y= FM×NQ求出即可;
FM×NQ求出即可;(3)根据△BDN∽△BFM求出DN=
 (-
(- x+12),求出CN=12-
x+12),求出CN=12-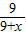 (-
(- x+12),根据平行四边形的性质得出方程-
x+12),根据平行四边形的性质得出方程- x+12=12-
x+12=12-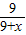 (-
(- x+12),求出方程的解即可.
x+12),求出方程的解即可.解答:解:(1)△CEM∽△CDB,△AFM∽△CDB,△ADC∽△CDB,△ACB∽△CDB;
(2)

过N作NQ⊥EF于Q,如图2,
∵据平移和矩形性质得出EF∥CD,EC∥FD,
∴四边形EFDC是矩形,
∴EC=DF=NQ=x,
∵△ACB中,∠ACB=90°,BC=15,AC=20,由勾股定理得:AB=25,
S△ACB=
 AB×CD=
AB×CD= AC×BC,
AC×BC,∴CD=12,由勾股定理得:AD=16,BD=9,
∵EF∥DC,
∴△AMF∽△ACD,
∴
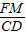 =
=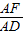 ,
,∴
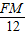 =
=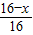 ,
,FM=-
 x+12,
x+12,∴y=
 FM×NQ=
FM×NQ= (-
(- x+12)x,
x+12)x,y=-
 x2+6x,
x2+6x,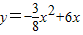 ,
,y=-
 (x-8)2+24,
(x-8)2+24,即当x=8时,△MNF的最大面积是24;
自变量x的取值范围是0<x<16,当x=8时,有最大值24;
(3)∵EF∥CD,
∴△BDN∽△BFM,
∴
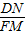 =
=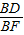 ,
,∴
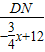 =
=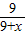 ,
,∴DN=
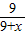 (-
(- x+12),
x+12),∴CN=12-DN=12-
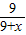 (-
(- x+12),
x+12),假设存在四边形MFNC为平行四边形,
此时CN=FM,
即-
 x+12=12-
x+12=12-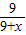 (-
(- x+12),
x+12),解得:x=6,
即在平移过程中存在四边形MFNC为平行四边形的情形,此时x的值是6.
点评:本题考查了相似三角形的性质和判定,矩形的性质和判定,平行四边形性质,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.

练习册系列答案
相关题目
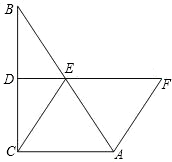 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=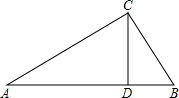 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=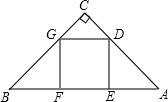 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为