��Ŀ����
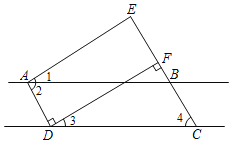
����Ŀ����ͼ����֪AD��DF��EC��DF����1����3����2����4����֤��AE��DF������������Ľ����̵Ŀո�����ջ�����������д���ɣ�
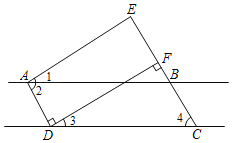
֤������AD��DF��EC��DF������֪��
���BFD����ADF��90������ ��
��EC�� ��
���EBA��_____����ֱ��ƽ�У��ڴ�����ȣ�
�ߡ�2����4������֪��
���EBA����4��������������
��AB��_____���� ��
���2+��ADC��180������ ��
���2+��ADF+��3��180����
�ߡ�1����3������֪��
���2+��ADF+��1��180����������������
��_____+��ADF��180����
��AE��DF���� ��
���𰸡�������.
��������
�����ڴ��������ֱ��ƽ�У��õ�EC��AD��������ֱ��ƽ�У��ڴ�����ȣ��ó���EBA����2�����������õ���EBA����4������ͬλ�������ֱ��ƽ�У��õ�AB��CD��������ֱ��ƽ�У�ͬ���ڽǻ����õ���2+��ADC��180�������������õ���EAD+��ADF��180�����ٸ���ͬ���ڽǻ�������ֱ��ƽ�еõ�AE��DF��
֤��������AD��DF��EC��DF������֪��
���BFD����ADF��90������ֱ�Ķ��壩��
��EC��AD���ڴ�����ȣ���ֱ��ƽ�У���
���EBA����2����ֱ��ƽ�У��ڴ�����ȣ�
�ߡ�2����4������֪��
���EBA����4��������������
��AB��DC��ͬλ����ȣ���ֱ��ƽ�У���
���2+��ADC��180������ֱ��ƽ�У�ͬ���ڽǻ�������
���2+��ADF+��3��180����
�ߡ�1����3����֪����
���2+��ADF+��1��180����������������
���EAD+��ADF��180����
��AE��DF��ͬ���ڽǻ�������ֱ��ƽ�У���
�ʴ�Ϊ����ֱ�Ķ��壬AD����2��CD��ͬλ����ȣ���ֱ��ƽ�У���ֱ��ƽ�У�ͬ���ڽǻ�������EAD��ͬ���ڽǻ�������ֱ��ƽ�У�