题目内容
【题目】已知![]() ,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.当∠APB=45°时,PD的长是( );
,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.当∠APB=45°时,PD的长是( );

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
【答案】A
【解析】
过P作PB的垂线,过A作PA的垂线,两条垂线相于与E,连接BE,由∠APB=45°可得∠EPA=45°,可得△PAE是等腰直角三角形,即可求出PE的长,根据角的和差关系可得∠EAB=∠PAD,利用SAS可证明△PAD≌△EAB,可得BE=PD,利用勾股定理求出BE的长即可得PD的长.
过P作PB的垂线,过A作PA的垂线,两条垂线相交与E,连接BE,
∵∠APB=45°,EP⊥PB,
∴∠EPA=45°,
∵EA⊥PA,
∴△PAE是等腰直角三角形,
∴PA=AE,PE=![]() PA=2,
PA=2,
∵四边形ABCD是正方形,
∴∠EAP=∠DAB=90°,
∴∠EAP+∠EAD=∠DAB+∠EAD,即∠PAD=∠EAB,
又∵AD=AB,PA=AE,
∴△PAD≌△EAB,
∴PD=BE=![]() =
=![]() =2
=2![]() ,
,
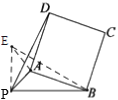
故选A.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目