题目内容
 如图,∠C=∠ADE=70°,∠B=∠E=30°,BC=ED,点D在BC上,那么将△ABC绕着点A按________时针方向旋转________度就能与△AED重合.
如图,∠C=∠ADE=70°,∠B=∠E=30°,BC=ED,点D在BC上,那么将△ABC绕着点A按________时针方向旋转________度就能与△AED重合.
顺 40°
分析:由∠C=∠ADE=70°,∠B=∠E=30°,BC=ED,得到△ABC≌△AED,则AD=AC,而∠C=70°,利用三角形的内角和定理可得到∠CAD=180°-70°-70°=40°,所以△ABC绕着点A顺时针旋转40°能与△AED重合.
解答:∵∠C=∠ADE=70°,∠B=∠E=30°,BC=ED,
∴△ABC≌△AED,
∴AD=AC,
而∠C=70°,
∴∠CAD=180°-70°-70°=40°,
∴△ABC绕着点A顺时针旋转40°能与△AED重合.
故答案为:顺,40°.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了三角形全等的判定与性质和等腰三角形的性质.
分析:由∠C=∠ADE=70°,∠B=∠E=30°,BC=ED,得到△ABC≌△AED,则AD=AC,而∠C=70°,利用三角形的内角和定理可得到∠CAD=180°-70°-70°=40°,所以△ABC绕着点A顺时针旋转40°能与△AED重合.
解答:∵∠C=∠ADE=70°,∠B=∠E=30°,BC=ED,
∴△ABC≌△AED,
∴AD=AC,
而∠C=70°,
∴∠CAD=180°-70°-70°=40°,
∴△ABC绕着点A顺时针旋转40°能与△AED重合.
故答案为:顺,40°.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了三角形全等的判定与性质和等腰三角形的性质.

练习册系列答案
相关题目
 如图,△ABC∽△ADE,若∠ADE=∠B,那么∠C=
如图,△ABC∽△ADE,若∠ADE=∠B,那么∠C=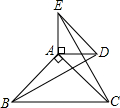 已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.
已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°. 如图,△ABC≌△ADE,若AD=AB,AE=AC,则另一组相等的边为
如图,△ABC≌△ADE,若AD=AB,AE=AC,则另一组相等的边为 如图,△ABC≌△ADE,则,AB=
如图,△ABC≌△ADE,则,AB= 如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于
如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于