题目内容
Rt△ABC中,∠C=90°,AC=6,AB=10,⊙C于AB相切,且⊙A、⊙C相切,则⊙A半径为________.
1.2或10.8
分析:利用勾股定理求得BC=8;然后根据三角形的面积公式求得点C距AB的距离,即⊙C的半径;最后由①两圆相外切的性质知⊙A、⊙C的半径之和为AC的长度;②两圆相内切的性质知⊙A、⊙C的半径之差为AC的长度.
解答:设以C为圆心的圆与AB相切于点D,⊙A的半径为r.
根据切线的性质知,CD是圆C的半径,也是直角三角形斜边上的高,
由勾股定理知,BC=8,
又因为S△ABC= AC•BC=
AC•BC= AB•CD,即6×8=10CD,
AB•CD,即6×8=10CD,
解得,CD=4.8;
①当⊙A、⊙C相外切时,4.8+r=AC,即4.8+r=6,解得,r=1.2;
②当⊙A、⊙C相内切时,r-4.8=AC,即r-4.8=6,解得,r=10.8;
故答案是:1.2或10.8.
点评:本题考查了切线的性质、两相切圆的性质.解题时,采用了“分类讨论”的数学思想,以防漏解.
分析:利用勾股定理求得BC=8;然后根据三角形的面积公式求得点C距AB的距离,即⊙C的半径;最后由①两圆相外切的性质知⊙A、⊙C的半径之和为AC的长度;②两圆相内切的性质知⊙A、⊙C的半径之差为AC的长度.
解答:设以C为圆心的圆与AB相切于点D,⊙A的半径为r.
根据切线的性质知,CD是圆C的半径,也是直角三角形斜边上的高,
由勾股定理知,BC=8,
又因为S△ABC=
 AC•BC=
AC•BC= AB•CD,即6×8=10CD,
AB•CD,即6×8=10CD,解得,CD=4.8;
①当⊙A、⊙C相外切时,4.8+r=AC,即4.8+r=6,解得,r=1.2;
②当⊙A、⊙C相内切时,r-4.8=AC,即r-4.8=6,解得,r=10.8;
故答案是:1.2或10.8.
点评:本题考查了切线的性质、两相切圆的性质.解题时,采用了“分类讨论”的数学思想,以防漏解.

练习册系列答案
相关题目
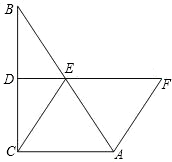 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=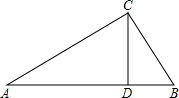 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=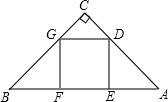 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为