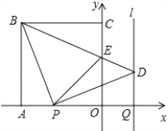
��Ŀ����
����Ŀ���涨�������ɸ���ͬ������������������ 0���ij������������������ 2��2��2������3���£���3���£���3���£���3���ȣ�����������ij˷������ǰ�2��2��2����2����������2��Ȧ 3 �η���������3���£���3���£���3���£���3����������3������������������3����Ȧ 4 �η�����һ��أ���![]() ������ a������ ��a ��Ȧ n�η���
������ a������ ��a ��Ȧ n�η���
������̽����
��1��ֱ��д����������2��������![]() ������
������
������˼����
2��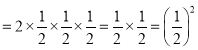
����֪�����������ļ����������ת��Ϊ�ӷ����㣬�����������ת��Ϊ�˷����㣬�������ij����������ת��Ϊ�˷������أ�
��2����һ�ԣ������������ʽ��������������ֱ��д���ݵ���ʽ��5��������![]() ������
������
��3�����룺������ a��a��0����Ȧn��n��3���η�д���ݵ���ʽ���ڶ��٣�
(4)Ӧ�ã���-3��8����-3����-����![]() ��9������
��9������![]() ����
����
���𰸡���1��![]() ��-2����2����
��-2����2����![]() ��4������2��8����3��
��4������2��8����3��![]() ����4��
����4��![]() .
.
��������
��1���ֱ𰴹�ʽ���м��㼴�ɣ�
��2���ѳ�����Ϊ�˷�����һ�������䣬�ӵڶ�������ʼ���α�Ϊ�������ɴ˷ֱ�ó������
��3�����ǰ���������Ϊ1���������������������Ϊ![]() ����a=a��(
����a=a��(![]() )n-1��
)n-1��
��4�����ڶ��ʵĹ��ɴ�����㣬ע������˳��
�⣺��1��2��=2��2��2=![]() ������
������![]() ����=��
����=��![]() ������
������![]() ��������
��������![]() ��=��2��
��=��2��
��2��5��=5��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() =��
=��![]() ��4��ͬ���ã�����
��4��ͬ���ã�����![]() ����=����2��8��
����=����2��8��
��3��a=a��![]() ��
��![]() ������
������ ��
��
(4)��-3��8����-3����-����![]() ��9������
��9������![]() ����
����
=��-3��8����![]() ��7 -����
��7 -����![]() ��9����-2��6
��9����-2��6
=-3-(-![]() )3
)3
=-3+![]()
=![]() .
.

 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�����Ŀ��ѧУʳ�ó���������������ذڷ���������ͬ����ĵ��ӣ����ӵĸ�������ӵĸ߶ȵĹ�ϵ���±���
���ӵĸ��� | ���ӵĸ߶ȣ���λ��cm�� |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
�� | �� |

��1���������Ϸ���x����������ʱ����д����ʱ���ӵĸ߶ȣ��ú�x��ʽ�ӱ�ʾ����
��2���ֱ�����������Ͽ���������ͼ����ͼ��ʾ������ʦ����������������һ���������һ����ĸ߶ȣ�