Question

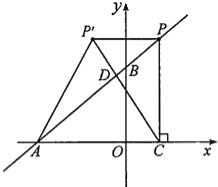
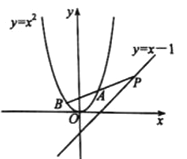
【题目】如图，点P在直线y=x-1上，设过点P的直线交抛物线y=x2于A(a，a2)，B(b，b2)两点，当满足PA=PB时，称点P为“优点”.

(1)当a+b=0时，求“优点”P的横坐标；

(2)若“优点”P的横坐标为3，求式子18a-9b的值；

(3)小安演算发现：直线y=x-1上的所有点都是“优点”，请判断小安发现是否正确？如果正确，说明理由；如果不正确，举出反例.

Answer 1

【答案】(1)点横坐标为；(2)27；(3)正确，理由见解析.

【解析】

（1）先判断点A与点B关于y轴对称得到PA∥x轴，所以P点的纵坐标为a2，P点的横坐标为a2+1，则利用PA=AB得到a2+1-a=a-（-a），然后求出a得到优点”P的横坐标；
（2）由于A点为PB的中点，根据线段的中点坐标公式得到a=，即2a-b=3，然后利用整体代入的方法计算代数式的值；

（3）设P（x，x-1），利用A点为PB的中点得到a=，a2=，消去a得到方程x2+2（b-1）x+1-b2=0，然后通过证明此方程一定有解判断直线y=x-1上的所有点都是“优点”．

(1)∵，

∴点、关于对称，

∴轴，

∵，

∴点的横坐标为，

∴点的坐标为，点的坐标为，

∵轴，

∴，解得，

∴点横坐标为；

(2)∵点在直线上，

∴点坐标为，

∵，

∴，

∴，

∴；

(3)设点坐标为，结合点的坐标，

当时，分析出点的坐标为，

把点坐标代入抛物线解析式中，

，

整理，得，

∵，

∴对于任意，总有x使得PA=AB，

∴直线上的点均为优点.