题目内容
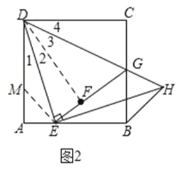
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.

【答案】(1)详见解析;(2)![]() ,理由详见解析
,理由详见解析
【解析】
1)如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,可得结论;
(2)如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角△AEM得:![]() ,得结论;
,得结论;
证明:(1)如图1,连接![]() ,
,
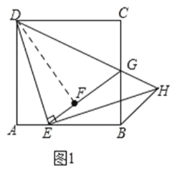
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]()
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ;
;
(2)![]() ,理由是:
,理由是:
如图2,在线段![]() 上截取
上截取![]() ,使
,使![]() ,
,
∵![]() ,
,
∴![]() ,
,
由(1)知:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
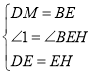
∴![]() ≌
≌![]()
∴![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;

练习册系列答案
相关题目