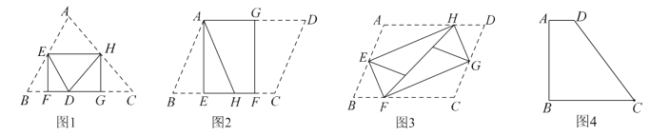
题目内容
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图: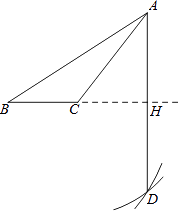
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是 . 他的依据是 .
【答案】小明;到线段两个端点距离相等的点在线段的垂直平分线上(两点确定一条直线)
【解析】解:如图,连接CD、BD,

∵CA=CD,BA=BD,
∴点C、点B在线段AD的垂直平分线上,
∴直线BC是线段AD的垂直平分线,
即BH⊥AD且平分AD,故小明的说法正确.
而CA不一定平分∠BDA,故小丽的说法错误;点C不一定为BH的中点,故小强的说法错误.
故答案为:小明;到线段两个端点距离相等的点在线段的垂直平分线上;两点确定一条直线.
由作图知CA=CD,BA=BD,点C、点B在线段AD的垂直平分线上,经过两点有且只有一条直线知道直线BC是线段AD的垂直平分线。

【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
【题目】有这样一个问题:探究函数y= ![]() 的图象与性质,小静根据学习函数的经验,对函数y=
的图象与性质,小静根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整: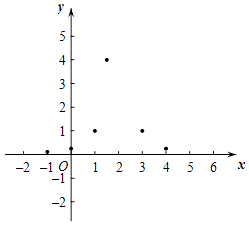
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下表是y与x的几组对应值.
x | … | ﹣1 | 0 | 1 |
|
| 3 | 4 | … |
y | … |
|
| 1 | 4 | m | 1 |
| … |
表中的m=;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质: .