题目内容
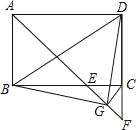
【题目】如图,在ABCD中,AD>AB,AM、BN、CP、DQ为四个内角的角平分线,P、为AD边上两点,其中AM与DQ相交于E,BN与CP相交于F,AM与BN相交于G,CP与DQ相交于H.
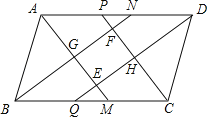
(1)求证:四边形EHFG是矩形.
(2)ABCD满足 时,四边形EHFG为正方形;ABCD满足 时,F点落在AD边上.(与点P、点N重合)
(3)探究矩形EHFG的对角线长度与ABCD的边长之间的数量关系,并证明.
【答案】(1)见解析; (2)∠BAD=90°,且BC=2AB ;BC=2AB;(3)GH=BC﹣AB;证明见解析.
【解析】
(1)根据平行线的性质及角平分线的定义证明四边形EHFG有三个角是直角即可;
(2)由(1)可得,四边形EHFG是矩形,若四边形EHFG为正方形,则有一组临边相等即可;若F点落在AD边上.(与点P、点N重合),则可得由(1)得:AF=AB,DF=CD,AG⊥BN,利用平行四边形的性质等量代换即可得到AB与BC的关系.
(3)连接EF、GH,由(1)(2)结论证四边形BQDN是平行四边形,四边形GHQB是平行四边形,即可得到其数量关系.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∵AM,BN分别平分∠DAB,∠ABC,
∴∠MAB+∠NBA=![]() (∠DAB+∠ABC)=×180°=90°.
(∠DAB+∠ABC)=×180°=90°.
∴∠EGF=∠AGB=90°,
同理:∠EHF=90°,∠GEH=90°,
∴四边形EHFG是矩形;
(2)ABCD满足∠BAD=90°,且BC=2AB时,四边形EHFG为正方形;理由如下:
此时F点落在AD边上,与点P、点N重合,如图1所示:
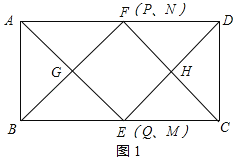
由(1)得:四边形EHFG是矩形,AG⊥BN,
∵AD∥BC,
∴∠AFB=∠CBF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠AFB=∠ABF,
∴AF=AB,
同理:DF=CD,
∴AF=AB=BE,
∵∠BAD=90°,
∴△BAF、△ABE是等腰直角三角形,
∵AE⊥BF,
∴BG=FG,AG=EG,
∴AG=![]() BF=BG=FG,
BF=BG=FG,
∴FG=EG,
∴四边形EHFG为正方形,
故答案为:∠BAD=90°,且BC=2AB;
ABCD满足BC=2AB时,F点落在AD边上.(与点P、点N重合);理由如下:
如图2所示:
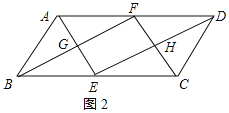
由(1)得:AF=AB,DF=CD,AG⊥BN,
∴AF=DF=AB,
∴AD=2AB,
∴BC=2AB,
故答案为:BC=2AB;
(3)矩形EHFG的对角线长度与ABCD的边长之间的数量关系为GH=BC﹣AB;理由如下:如图3所示:连接EF、GH
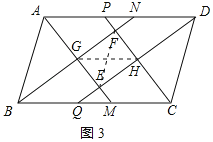
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∵四边形EHFG是矩形,
∴GH=EF,BN∥DQ,
∴四边形BQDN是平行四边形,
∴BN=DQ,
同(1)(2)得:AG⊥BN,AN=AB,CQ=CD=AB,
∴BG=NG,
同理:
∴BG=QH,
∴四边形GHQB是平行四边形,
∴GH=BQ=BC﹣CQ=BC﹣AB.