题目内容
已知：三条直线l1、l2、l3，l1∥l2，l2∥l3，求证：l1∥l3，若用反证法证明该题，第一步应假设
l1与l3不平行，则设相交于点A
l1与l3不平行，则设相交于点A
．分析：由于反证法的步骤是首先假设结论不成立，进而得出答案．
解答：解：∵求证：l1∥l3，若用反证法证明该题，则需要从结论的反面出发，
∴第一步应假设l1与l3不平行，则设相交于点A．
故答案为：l1与l3不平行，则设相交于点A．
∴第一步应假设l1与l3不平行，则设相交于点A．
故答案为：l1与l3不平行，则设相交于点A．
点评：本题考查了反证法，注意逆命题的与原命题的关系是解题关键．
练习册系列答案
相关题目
如图，已知△ABC中，∠ABC=90°，AB=BC，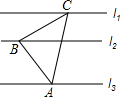
如图，已知△ABC中，∠ABC=90°，AB=BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2，l2，l3之间的距离为3，则△ABC面积为（ ）
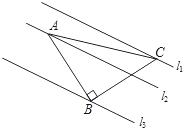如图，已知△ABC中，∠ABC=90°，AB=BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2，l2，l3之间的距离为3，则AC的长是（ ）