题目内容
9. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C的面积比为4:9.设B点的对应点B′的横坐标是2,则点B的横坐标是-3.
如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C的面积比为4:9.设B点的对应点B′的横坐标是2,则点B的横坐标是-3.
分析 过B和B′向x轴引垂线,构造相似比为2:3的相似三角形,那么利用相似比和所给B′的横坐标即可求得点B的横坐标.
解答 解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴$\frac{CD}{EC}$=$\frac{BC}{B′C}$,
又∵△ABC的位似图形△A′B′C的面积比为4:9,
∴$\frac{BC}{B′C}$=$\frac{2}{3}$,
∴$\frac{CD}{CE}$=$\frac{2}{3}$,
又∵点B'的横坐标是2,点C的坐标是(-1,0),
∴CE=3,
∴CD=$\frac{2}{3}$×3=2,
∴OD=3,
∴点B的横坐标为:-3.
故答案为:-3.
点评 本题考查了位似变换,坐标与图形的性质,根据相似三角形的性质求出是解题的关键.

练习册系列答案
相关题目
1.已知A,B,C在一条直线上,AB=10,AC=6,那么AB的中点与AC的中点的距离为( )
| A. | 8 | B. | 2或8 | C. | 2 | D. | 6 |
 如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,∠AGE与∠E相等吗?为什么?
如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,∠AGE与∠E相等吗?为什么?


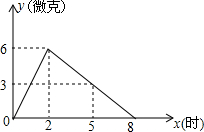 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,那么当成人按规定剂量服药后,根据图象回答下列问题:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,那么当成人按规定剂量服药后,根据图象回答下列问题: