题目内容
如图,一次函数y=| 1 |
| 2 |
| k |
| x |
 标为4.
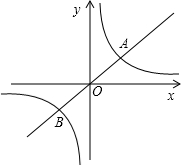
标为4.(1)求A,B两点的坐标及k的值;
(2)根据图象求出使一次函数的值大于反比例函数的值的x的取值范围;
(3)若反比例函数图象上一点C的纵坐标为8,求△AOC的面积.
分析:(1)由于A、B两点关于原点对称,将A点横坐代入一次函数求得纵坐标,再把A点坐标代入反比例函数求得k的值.
(2)由图象可看出,即当一次函数图象在反比例函数图象上面时x的取值范围.
(3)先由反比例函数解析式求得C点的坐标,然后由A、C、O求得AC及O到AC的距离,最后求得△AOC的面积.
(2)由图象可看出,即当一次函数图象在反比例函数图象上面时x的取值范围.
(3)先由反比例函数解析式求得C点的坐标,然后由A、C、O求得AC及O到AC的距离,最后求得△AOC的面积.
解答:解:(1)将A点坐标代入一次函数求得A(4,2),代入反比例函数可求得k=4×2=8.
又A、B两点关于原点对称,则B点坐标为(-4,-2).
(2)由图象可以看出,当x>4或-4<x<0时,一次函数的值大于反比例函数的值.
(3)将C点的纵坐标代入y=
求得C点坐标为(1,8),则|AC|=
=3
.
又由A、C两点可求得直线AC的解析式为y=-2x+10,则点0到AC的距离d=
=2
.
所以△AOC的面积S=
|AC|d=
×3
×2
=15.
又A、B两点关于原点对称,则B点坐标为(-4,-2).
(2)由图象可以看出,当x>4或-4<x<0时,一次函数的值大于反比例函数的值.
(3)将C点的纵坐标代入y=
| 8 |
| x |
| (4-1)2+(2-8)2 |
| 5 |
又由A、C两点可求得直线AC的解析式为y=-2x+10,则点0到AC的距离d=
| |-10| | ||
|
| 5 |
所以△AOC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查了反比例函数图象上点的坐标特征及由点的坐标确定三角形的面积,综合性较强.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数