Question

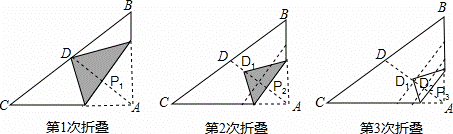
如图，直角三角形纸片ABC中，AB=3，AC=4，D为斜边BC中点，第1次将纸片折叠，使点A与点D重合，折痕与AD交与点P₁；设P₁D的中点为D₁，第2次将纸片折叠，使点A与点D₁重合，折痕与AD交于点P₂；设P₂D₁的中点为D₂，第3次将纸片折叠，使点A与点D₂重合，折痕与AD交于点P₃；…；设P_n﹣1D_n﹣2的中点为D_n﹣1，第n次将纸片折叠，使点A与点D_n﹣1重合，折痕与AD交于点P_n（n＞2），则AP₆的长为（　　）

　 A．                           B．                       C．    D．   

Answer 1

考点：翻折变换（折叠问题）。

解答：解：由题意得，AD=BC=，AD₁=AD﹣DD₁=，AD₂=，AD₃=，AD_n=，

故AP₁=，AP₂=，AP₃=…APn=，

故可得AP₆=。

故选A。