题目内容
一个多边形的所有内角和与其中一个外角的度数和为1370°,则该多边形的边数为
- A.7
- B.8
- C.9
- D.10
C
分析:根据n边形的内角和定理可知:n边形内角和为(n-2)×180°.设这个外角度数为x度,利用方程即可求出答案.
解答:设这个外角度数为x,根据题意,得
(n-2)×180°+x=1370°,
解得:x=1370°-180°n+360°=1730°-180°n,
由于0<x<180°,即0<1730°-180°n<180°,
解得8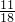 <n<9
<n<9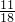 ,
,
所以n=9.
故多边形的边数是9.
故选C.
点评:主要考查了多边形的内角和定理.n边形的内角和为:180°•(n-2).
分析:根据n边形的内角和定理可知:n边形内角和为(n-2)×180°.设这个外角度数为x度,利用方程即可求出答案.
解答:设这个外角度数为x,根据题意,得
(n-2)×180°+x=1370°,
解得:x=1370°-180°n+360°=1730°-180°n,
由于0<x<180°,即0<1730°-180°n<180°,
解得8
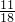 <n<9
<n<9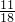 ,
,所以n=9.
故多边形的边数是9.
故选C.
点评:主要考查了多边形的内角和定理.n边形的内角和为:180°•(n-2).

练习册系列答案
相关题目