题目内容
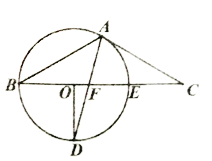
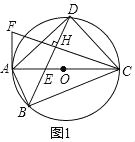
【题目】已知四边形ABCD为⊙O的内接四边形,直径AC与对角线BD相交于点E,作CH⊥BD于H,CH与过A点的直线相交于点F,∠FAD=∠ABD.
(1)求证:AF为⊙O的切线;
(2)若BD平分∠ABC,求证:DA=DC;
(3)在(2)的条件下,N为AF的中点,连接EN,若∠AED+∠AEN=135°,⊙O的半径为2![]() ,求EN的长.
,求EN的长.
【答案】(1)见解析;(2)见解析;(3)NE=![]()
【解析】
(1)欲证明AF为⊙O的切线,只需推知CA⊥AF;
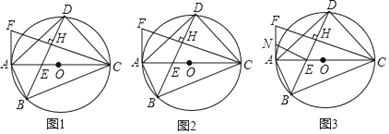
(2)如图2,连接OD.理由圆周角定理和等量代换推知:∠DOA=∠DOC,则DA=DC.
(3)如图3,连接OD交CF于M,作EP⊥AD于P.构造全等三角形:△ODE≌△OCM,则OE=OM,设OM=m,所以AE=2![]() ﹣m,AP=PE=2﹣
﹣m,AP=PE=2﹣![]() m,DP=2+
m,DP=2+![]() m;由△EAN∽△DPE的对应边成比例推知:
m;由△EAN∽△DPE的对应边成比例推知:![]() =
=![]() ,所以
,所以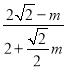 =
=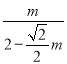 ,求出m=
,求出m=![]() ,得到AN=
,得到AN=![]() ,AE=
,AE=![]() ,结合勾股定理得NE=
,结合勾股定理得NE=![]() .
.
(1)证明:如图1,∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠DCA=90°.
∵![]() ,
,
∴∠ABD=∠DCA,
∵∠FAD=∠ABD,
∴∠FAD=∠DCA,
∴∠FAD+∠DCA=90°,
∴CA⊥AF,
∴AF为⊙O的切线.
(2)证明:如图2,连接OD,
∵![]() ,
,
∴∠ABD=![]() ∠AOD,
∠AOD,
∵![]() ,
,
∴∠DBC=![]() ∠DOC,
∠DOC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠DOA=∠DOC,
∴DA=DC.
(3)如图3,连接OD交CF于M,作EP⊥AD于P,
∵AC为⊙O的直径,
∴∠ADC=90°.
∵DA=DC,
∴DO⊥AC,
∴∠FAC=∠DOC=90°,
∴AF∥OM,
∵AO=OC,
∴OM=![]() AF.
AF.
∵∠ODE+∠DEO=90°,∠OCM+∠DEO=90°.
∴∠ODE=∠OCM.
∵∠DOE=∠COM,OD=OC,
∴∴△ODE≌△OCM,
∴OE=OM,
设OM=m,
∴AE=2![]() ﹣m,AP=PE=2﹣
﹣m,AP=PE=2﹣![]() m,DP=2+
m,DP=2+![]() m,
m,
∵∠AED+∠AEN=135°,∠AED+∠ADE=135°,
∴∠AEN=∠ADE,
∵∠EAN=∠DPE,
∴△EAN∽△DPE,
∴![]() =
=![]() ,
,
∴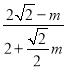 =
=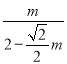 ,
,
∴m=![]() ,
,
∴AN=![]() ,AE=
,AE=![]() ,
,
∴勾股定理得NE=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案