Question

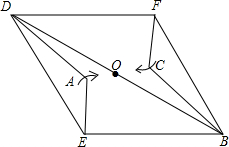如图，已知：?ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形．
求证：四边形ABCD是矩形．

Answer 1

考点：翻折变换（折叠问题）,平行四边形的性质,矩形的判定

专题：证明题

分析：先根据菱形的性质得BD⊥EF，则∠DOE=90°，再根据折叠的性质得到∠DAE=∠DOE=90°，由于四边形ABCD为平行四边形，根据矩形的判定方法即可得到
四边形ABCD是矩形．

解答：证明：如图，
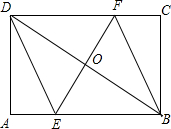∵四边形DEBF为菱形，
∴BD⊥EF，
∴∠DOE=90°，
∵沿DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，
∴∠DAE=∠DOE=90°，
∵四边形ABCD为平行四边形，
∴四边形ABCD是矩形．

点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了平行四边形的性质和矩形的判定．