Question

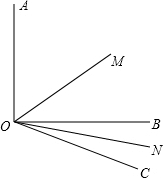
如图所示已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC；
（1）∠MON=

45

°；
（2）∠AOB=α，∠BOC=β，求∠MON的度数；并从你的求解你能看出什么什么规律吗？

Answer 1

分析：（1）根据题意可知，∠AOC=120°，由OM平分∠AOC，ON平分∠BOC；推出∠MOC=∠AOC=60°，∠CON=

1

2

∠BOC=15°，由图形可知，∠MON=∠MOC-∠CON，即∠MON=45°；
（2）同理可得，∠MOC=

1

2

（α+β），∠CON=

1

2

β，根据图形便可推出∠MON=∠MOC-∠CON=

1

2

（α+β）-

1

2

β=

α

2

．

解答：解：（1）∵∠AOB=90°，∠BOC=30°，
∴∠AOC=∠AOB+∠BOC=90°+30°=120°，
∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC=∠AOC=60°，∠CON=

1

2

∠BOC=15°，
∴∠MON=∠MOC-∠CON=60°-15°=45°；
故答案为：45°
（2）同理可得，∠MOC=

1

2

（α+β），∠CON=

1

2

β，
∴∠MON=∠MOC-∠CON=

1

2

（α+β）-

1

2

β=

α

2

．
则得出规律为∠MON=

1

2

∠AOB．

点评：本题主要考查角平分线的性质，角的度数的计算，关键在于运用数形结合的思想推出∠AOC=∠AOB+∠BOC，∠MON=∠MOC-∠CON．