题目内容
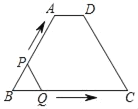
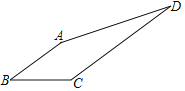
【题目】如图，在四边形ABCD中，AB∥CD，2AB=2BC=CD=10，tanB=
，则AD=______．
【答案】3
【解析】
过A作AF⊥CD于F，过C作CE⊥AB于E，根据矩形的性质得出AF=CE，AE=CF，求出AF和DF长，再根据勾股定理求出即可．
∵2AB=2BC=CD=10，
∴AB=BC=5，
过A作AF⊥CD于F，过C作CE⊥AB于E，
则∠AEC=∠AFD=∠BEC=90°，AF∥CE，
∵AB∥CD，
∴四边形AECF是矩形，
∴AE=CF，AF=CE，
∵在Rt△BEC中，tanB=
，
又∵BC=5，
CE=3，BE=4，
∴AE=CF=5-4=1，AF=CE=3，
∵CD=10，
∴DF=10-1=9，
在Rt△AFD中，由勾股定理得：AD=
=3
，
故答案为：
．
练习册系列答案
阅读快车系列答案
相关题目
