题目内容
在反比例函数y=
(k<0)的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则y1与y2的大小关系是
| k | x |
y1>y2
y1>y2
.分析:先根据反比例函数y=
中k<0可判断出此函数图象在二、四象限,再根据x1<0<x2,可判断出A、B两点所在的象限,根据各象限内点的坐标特点即可判断出y1与y2的大小关系.
| k |
| x |
解答:解:∵反比例函数y=
中k<0,
∴此函数图象在二、四象限,
∵x1<0<x2,
∴A(x1,y1)在第二象限;点B(x2,y2)在第四象限,
∴y1>0>y2,
∴y1>y2.
故答案为:y1>y2.
| k |
| x |
∴此函数图象在二、四象限,
∵x1<0<x2,
∴A(x1,y1)在第二象限;点B(x2,y2)在第四象限,
∴y1>0>y2,
∴y1>y2.
故答案为:y1>y2.
点评:本题考查的是反比例函数图象上点的坐标特点及各象限内点的坐标特点,先根据k<0判断出该函数图象所在象限是解答此题的关键.

练习册系列答案
相关题目
已知点(3,6)在反比例函数y=
(k≠0)的图象上,那么下列各点中在此函数图象上的点是( )
| k |
| x |
| A、(-3,6) |
| B、(3,-6) |
| C、(2,-9) |
| D、(2,9) |
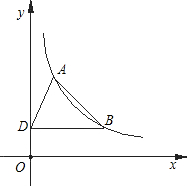 点B作y轴的垂线,垂足为D,连接AD.
点B作y轴的垂线,垂足为D,连接AD. (2013•西宁)如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数
(2013•西宁)如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数 (2013•泉州质检)如图,在方格纸中(小正方形的边长为1),直线AB与两坐标轴交于格点A、B,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(2013•泉州质检)如图,在方格纸中(小正方形的边长为1),直线AB与两坐标轴交于格点A、B,根据所给的直角坐标系(O是坐标原点),解答下列问题: