Question

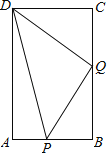
【题目】如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动．问：

（1）几秒时△PBQ的面积等于8cm2；

（2）几秒时△PDQ的面积等于28cm2；

（3）几秒时PQ⊥DQ．

Answer 1

【答案】（1）2秒或4秒后△PBQ的面积等于8cm2；

（2）2秒或4秒后△PDQ的面积等于28cm2；

（3）秒或6秒后PQ⊥DQ．

【解析】

（1）表示出PB，QB的长，利用△PBQ的面积等于8cm2列式求值即可；

（2）设出发秒x时△DPQ的面积等于28平方厘米，根据三角形的面积公式列出方程，再解方程即可；

（3）如果PQ⊥DQ，则∠DQP为直角，得出△BPQ∽△CQD，即可得出，再设AP＝x，QB＝2x，代入求出x即可．

（1）设x秒后△PBQ的面积等于8cm2．

则AP＝x，QB＝2x．

∴PB＝6﹣x．

∴×（6﹣x）2x＝8，

解得x1＝2，x2＝4，

答：2秒或4秒后△PBQ的面积等于8cm2；

（2）设出发秒x时△DPQ的面积等于8cm2．

∵S矩形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ＝S△DPQ

∴12×6﹣×12x﹣×2x（6﹣x）﹣×6×（12﹣2x）＝28，

化简整理得 x2﹣6x+8＝0，

解得x1＝2，x2＝4，

答：2秒或4秒后△PDQ的面积等于28cm2；

（3）设x秒后PQ⊥DQ时，则∠DQP为直角，

∴△BPQ∽△CQD，

∴，

设AP＝x，QB＝2x．

∴，

∴2x215x＋18＝0，

解得：x＝或6，

经检验x＝是原分式方程的根，x＝6不是原分式方程的根，

当x＝6时，P点到达B点、Q点到达C点，此时PQ⊥DQ．

答：秒或6秒后PQ⊥DQ．