Question

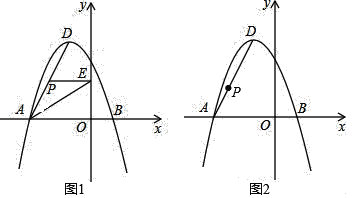
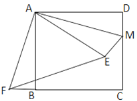
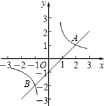
【题目】如图，直线y=x+m与双曲线相交于A（2，1）、B两点．

（1）求m及k的值；

（2）求出点B的坐标；并直接写出x取何值时，；

（3）P为直线x=上一点，当△ APB的面积为6时，请直接写出点P的坐标．

Answer 1

【答案】（1）m=-1，k=2 ；（2）B（-1，-2），-1＜x ＜0或x＞2；（3）（）或（，-）．

【解析】

（1）把A的坐标分别代入两函数的解析式即可求出答案；

（2）解由两函数组成的方程组，求出方程组的解，即可得出B的坐标；结合图象和两交点的横坐标即可得出答案；

（3）设直线x=与直线AB相交于点D（，y），则可求出y的值，得到D的坐标．设P（，b），由S△ABP= S△PAD +S△PDB =PD（ ）=6，解方程即可得到结论．

（1）∵把A（2，1）代入y=x+m得：1=2+m，∴m=﹣1．

∵把A（2，1）代入y得：1，∴k=2；

（2）∵解由y=x﹣1和y组成的方程组得：．

又∵A（2，1），∴B的坐标是（﹣1，﹣2）；由图像可知：时x的取值范围是﹣1＜x＜0或x＞2．

（3）设直线x=与直线AB相交于点D（，y），则y=，∴D（，）．

设P（，b），则S△ABP= S△PAD +S△PDB =PD（ ）=6，∴，解得：b=或b=，∴P的坐标为（）或（，）．