题目内容
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于C点,与x轴交于A、B两点,A点在B点左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD的面积的最大值;
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.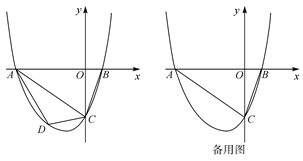
(1)∴y= x2+
x2+ x-3
x-3
(2)过点D作DM∥y轴分别交线段AC和x轴于点M、N.
∴S四边形ABCD=S△ABC+S△ACD= +
+ ·DM·(AN+ON)=
·DM·(AN+ON)= +2DM.
+2DM.
∵A(-4,0),C(0,-3),
设直线AC的解析式为y=kx+b,
代入求得:y=- x-3,
x-3,
令D ,M
,M ,
,
则DM=- x-3-
x-3- =-
=- (x+2)2+3.
(x+2)2+3.
当x=-2时,DM有最大值3,此时四边形ABCD面积有最大值 .
.
(3)如图①所示,讨论:①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,
∵C(0,-3),令 x2+
x2+ x-3=-3得x1=0,x2=-3,
x-3=-3得x1=0,x2=-3,
∴CP1=3.∴P1(-3,-3).
②如图②,平移直线AC交x轴于点E,交x轴上方的抛物线于点P,
当AC=PE时,四边形ACEP为平行四边形,
∵C(0,-3),
∴可令P(x,3),由 x2+
x2+ x-3=3得:x2+3x-8=0,
x-3=3得:x2+3x-8=0,
解得x1= 或x2=
或x2= ,
,
此时存在点P2 和P3
和P3 .
.
综上所述,存在3个点符合题意,坐标分别是P1(-3,-3),P2 ,P3
,P3 .
.
解析

练习册系列答案
相关题目


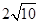 .
. 使得
使得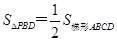 ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,