Question

【题目】在平面直角坐标系中，二次函数的图象与x轴交于A（－3，0），B（1，0）两点，与y轴交于点C．

（1）求这个二次函数的关系解析式；

（2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；

考生注意：下面的（3）、（4）、（5）题为三选一的选做题，即只能选做其中一个题目，多答时只按作答的首题评分，切记啊！

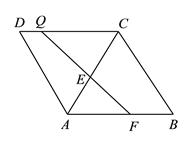
（3）在平面直角坐标系中，是否存在点Q，使△BCQ是以BC为腰的等腰直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；

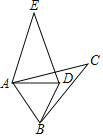
（4）点Q是直线AC上方的抛物线上一动点，过点Q作QE垂直于x轴，垂足为E．是否存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似？若存在，直接写出点Q的坐标；若不存在，说明理由；

（5）点M为抛物线上一动点，在x轴上是否存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由．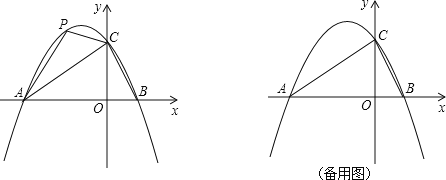

Answer 1

【答案】（1）；（2）存在，；（3）存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为：Q1(2,3),Q2(3,1),Q3(1,1),Q4(2,1)；（4）存在，Q点坐标为(2,2)或；（5）存在点Q,使以A. C.M、Q为顶点的四边形是平行四边形.Q点坐标为：.

【解析】

（1）将点A、B的坐标代入即可求得a、b，从而得到二次函数的关系解析式．

（2）设点P坐标为（m，n），则．连接PO，作PM⊥x轴于M，PN⊥y轴于N，根据求出S关于m的二次函数，根据二次函数最值求法即可求解．

（3）如图（3）所示，以BC为边，在线段BC两侧分别作正方形，正方形的其他四个顶点均可以使得“△BCQ是以BC为腰的等腰直角三角形”，因此有四个点符合题意要求；

（4）如图（4）所示，若以点B、Q、E为顶点的三角形与△AOC相似，有两种情况，需要分类讨论，不要漏解；

（5）以A、C、M、Q为顶点的四边形是平行四边形，有四种情况，分别如图（5）a、图（5）b所示，注意不要漏解．

解：（1）由抛物线过A（－3，0），B（1，0），则

，解得．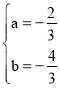

∴二次函数的关系解析式为．

（2）设点P坐标为（m，n），则．

连接PO，作PM⊥x轴于M，PN⊥y轴于N．

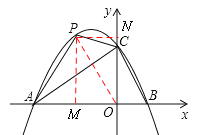
PM =，，AO=3．

当时，，所以OC=2．

∵＜0，∴函数有最大值，当时，有最大值．

此时．

∴存在点，使△ACP的面积最大．

(3)如图(3)所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3,则点Q1,Q2,Q3,Q4为符合题意要求的点.

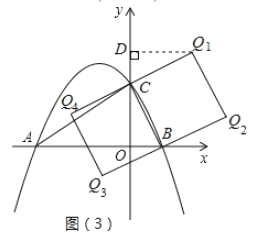
过Q1点作Q1D⊥y轴于点D，

∵∠BCQ1=90°，

∴∠Q1CD+∠OCB=90°，

又∵在直角△OBC中,∠OCB+∠CBO=90°，

∴∠Q1CD=∠OCB，

又∵Q1C=BC,∠Q1DC=∠BOC，

∴△Q1CD≌△CBO，

∴Q1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q1(2,3)；

同理求得Q2(3,1),Q3(1,1),Q4(2,1).

∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为：Q1(2,3),Q2(3,1),Q3(1,1),Q4(2,1).

(4)如图(4)所示,设E(n,0),则BE=1n, .

假设以点B.Q、E为顶点的三角形与△AOC相似，则有两种情况：

①若△AOC∽△BEQ,则有：，

即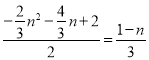,化简得：n2+n2=0，

解得n1=2,n2=1(与B重合,舍去),

∴n=2, .

∴Q(2,2)；

②若△AOC∽△BQE,则有：，

即,化简得：4n2n3=0，

解得 (与B重合,舍去),

∴.

综上所述，存在点Q，使以点B.Q、E为顶点的三角形与△AOC相似.

Q点坐标为(2,2)或.

(5)假设存在点Q，使以A. C.M、Q为顶点的四边形是平行四边形.

①若CM平行于x轴,如图(5)a所示,有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.

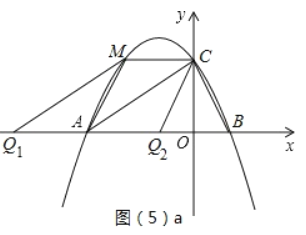
∵CM∥x轴,∴点M、点C(0,2)关于对称轴x=1对称，

∴M(2,2),

∴CM=2.

由Q1A=Q2A=CM=2,得到Q1(5,0),Q2(1,0)；

②若CM不平行于x轴,如图(5)b所示.过点M作MG⊥x轴于G，

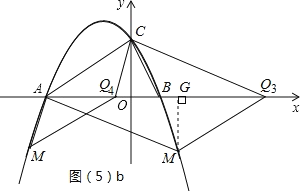
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=2.

设M(x,2),则有，

解得

又QG=3,

∴，

综上所述,存在点Q,使以A. C.M、Q为顶点的四边形是平行四边形.Q点坐标为：.