题目内容
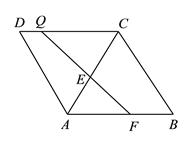
【题目】如图，菱形
的边
， 
， 
是
上一点， 
， 
是
边上一动点，将梯形
沿直线
折叠， 
的对应点为
，当
的长度最小时， 
的长为__________．
【答案】
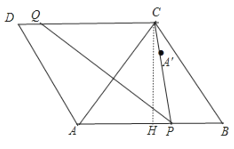
【解析】如图所示，过点
作
，交
于点
.
在菱形
中，
∵
，且
，所以
为等边三角形，
．
根据“等腰三角形三线合一”可得
，因为
，所以
．
在
中，根据勾股定理可得， 
．
因为梯形
沿直线
折叠，点
的对应点为
，根据翻折的性质可得，点
在以点
为圆心， 
为半径的弧上，则点
在
上时， 
的长度最小，此时
，因为
．
所以
，所以
，所以
．
点睛:A′为四边形ADQP沿PQ翻折得到，由题目中可知AP长为定值，即A′点在以P为圆心、AP为半径的圆上，当C、A′、P在同一条直线时CA′取最值，由此结合直角三角形勾股定理、等边三角形性质求得此时CQ的长度即可.
练习册系列答案
相关题目
